Электрическое напряжение между двумя плоскостями

Физика Электромагнетизм
1

2.24. Пространство между двумя плоскостями, отстоящими друг от друга на расстояние 2а, заполнено зарядом, объемная плотность которого зависит только от координаты x оси, перпендикулярной этим плоскостям, как \rho=\alpha x, где \alpha - постоянная. Начало координат (x=0) находится посередине между этими плоскостями. Найти зависимости от x напряженности электрического поля, точнее E_x(x) и E(x). Изобразить их примерные графики
решил задачу теоремой Гаусса

попробовал без гаусса вышло в \pi раз больше
пользовался следующими уравнениями

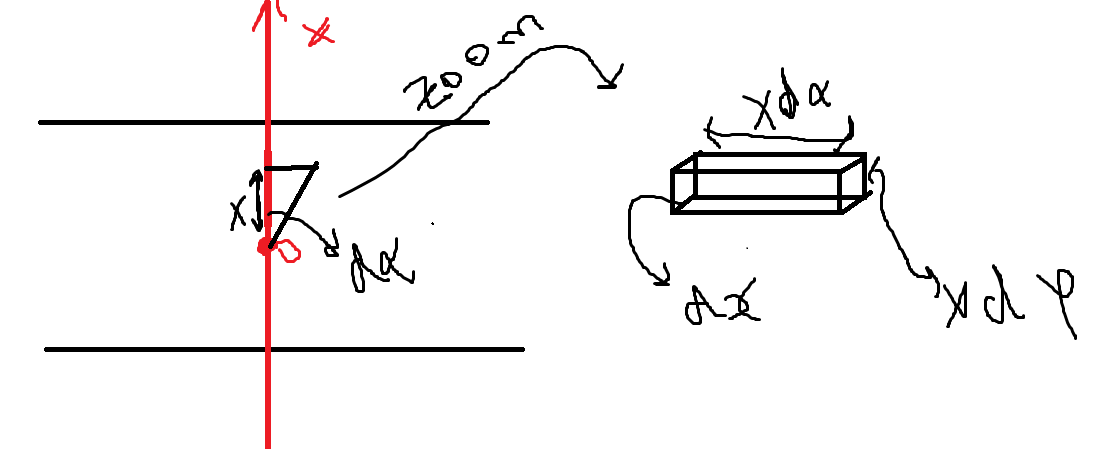
image
image1111×449 9.39 KB

dE = k dq/x^2
dq = ax xd\alpha x d \theta dx

  • потом интегрировал от 0 до 2 \pi для углов d \alpha d \theta
    в чем ошибка ?

  • ответ выходит E=ax^2/2E0

2
  1. Не спроецировал на ось икс
  2. Разделил в законе Кулона на x^2, якобы полагая, что расстояние от рассматриваемого заряда к началу координат равно x. (?)
  3. Неправильно расписал элемент объёма.
  4. Система координат (x,\alpha,\theta) взята неразумно. Лучше бы чисто в декартовых/цилиндрических/сферических решал.
2 лайка