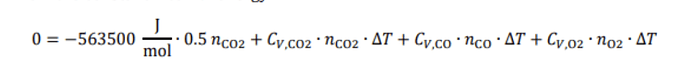В данной задаче я понял все, кроме одного. Я принял что изменение внутренней энергии равно нулю, ведь процесс как бы одновременно адиабатический и V= const. То есть w и q не изменяются, однако в решении они то принимают что dU=0, то принимают что dU=dH-(dn)RT. Почему они так могут делать?
3 лайка
А в чём противоречие?
1 лайк
Почему они пишут что change in internal energy equals 0, а потом показывают что dU= -563.5 kJ/mol?
Так там обозначение стандартных условий стоит… они посчитали для стандартных, чтобы использовать для условий задачи. В этом же вся термодинамика.
3 лайка
Понял. А почему в уравнении dU= nCvdT мы еще учитываем стандартную внутреннюю энергию? Я думал там берут U при двух температурах
P. S: Кажется я понял. Они взяли начальную как стандартную, а конечную как в нашей системе и получилось (?)
Так и делают.
1 лайк
Стандартные условия не фиксируют температуру. Стандартные условия можно при разных температурах брать.
Определения почитайте, что означает этот маленький “нолик” в обозначениях.
1 лайк
Я почитал и первая же строчка в Википедии отвечает на мой вопрос:
" In chemistry, the standard state of a material (pure substance, mixture or solution) is a reference point used to calculate its properties under different conditions"
Однако у меня появился другой вопрос. Почему мы можем использовать standard state для внутреней энергии тут, в уравнении для зависимости внутреней энергии от температуры. Разве если использовать разницу внутрених энергий при разных температурах, то их standard states не сократятся?
1 лайк
Это разные категории как теплое и мягкое, либо я не понимаю вопроса, т.к. вообще не понимаю что означает “сократятся стандартные состояния”.
Возможно я выражаюсь не особо корректно, сейчас попытаюсь объяснить:
В общем я понял разницу между внутренней энергией и стандартной внутренней энергией, но после этого я взглянул на это выражение
Для меня это выглядит как будто они берут deltaU- deltaU (стандартная) = nCv*deltaT, но в данном случае это же разное. Нельзя от обычно delta U отнимать delta U (стандартная), к тому же тогда выражение будет странным, ведь стандартные функции никак не зависят от температуры. В моем понимании они должны брать deltaU(T2) - deltaU(T1) и тогда т.к это одна и та же система, то у каждой deltaU будет одинаковый deltaU (стандартная) и на нее в принципе можно забить. То есть каждая deltaU отсчитываются от одной и той же deltaU (стандартная) и их разница уже никак не зависит от нее. Но тогда вопрос, а почему deltaU (стандартная) в этом выражении все таки присутствует?
Я писал выше, что зависят. Температура не фиксируется. Стандартные функции имеют зависимость от температуры. Я именно поэтому и сказал читать определение внимательно. Там надо было увидеть не только то, что там написано, и но то, что там не написано. По температуре условий не было. Например
\begin{gathered}
\Delta_r U^{\circ}_{373}=\Delta_r U^{\circ}_{298}+\int\limits_{298}^{373}\Delta_r C_v\, dT \\
\Delta_r H^{\circ}_{373}=\Delta_r H^{\circ}_{298}+\int\limits_{298}^{373}\Delta_r C_p\, dT \\
\Delta_r S^{\circ}_{373}=\Delta_r H^{\circ}_{298}+\int\limits_{298}^{373}\frac{\Delta_r C_p}{T}\, dT
\end{gathered}
Потому что мы вообще считаем не для реакции изменение, у нас сложный переход, где реакция лишь одна часть процесса.
Попробуй процесс перехода из начального состояния в конечное, разбить на сумму процессов, в котором один из них будет нужной реакцией в нужных нам условиях.
Тут еще есть нюанс, что \Delta_r U и \Delta U разные вещи, первая величина это производная второй величины по химической переменной. У них даже размерности разные т.е. они друг к другу относятся как скорость и путь, как сила тока и заряд и т.д. для некоторых величин критично важно в каких конкретно условиях мы считаем эту “скорость изменения переменной по мере протекания реакции” и поэтому мы указываем, что измерена эта “скорость” для стандартных условий.
3 лайка
Вау. Раньше я думал что хорошо знаю термодинамику, но сейчас понимаю что это вообще не так и надо перечитать книжки по ней, что бы реально начать понимать.
Я чет запутался вчера. Там даже в задаче дается стандартная энтальпия при 298 К и можно посчитать стандартную внутреннюю энергию при 298 К
Не особо понял как это сделать. Типо в начале присутствуют только реагенты и температура в реакторе 298К . Во время всего процесса объём фиксированные и равен 1 м^3. Далее происходит реакция. Повышается температура и уменьшается давление в реакторе. Затем мы приходим к равновесной смели когда у нас есть смесь продуктов и реагентов и т.к delta n = -1 , то давление упадет, а температура в конечной смеси соответственно поднимется. В конечной точке delta U = 0(как и в начале), ведь у нас V=const и dq= 0. То есть в ходе процесса у нас на dU влияет не только нагревание, но и реакция и поэтому ее мы тоже учитываем в уравнении, при этом delta U = 0 (левая сторона), подобно тому как мы учитываем нагревание, фазовые переходы и так далее в различных термодинамических циклах?
Как будто сначала полностью пройдет реакция, а потом уже полученная смесь будет нагреваться
Без повышения температуры реакцию надо проводить. Т.е. тепло отводить в этой стадии нужно, т.к. данные \Delta_r U^{\circ} даны для именно такого процесса.
условно как будто сначала до конца пройдет реакция, а только потом эта теплота вносится и нагревает систему?
1 лайк
Да, именно так.
1 лайк
Теперь понял. Спасибо вам