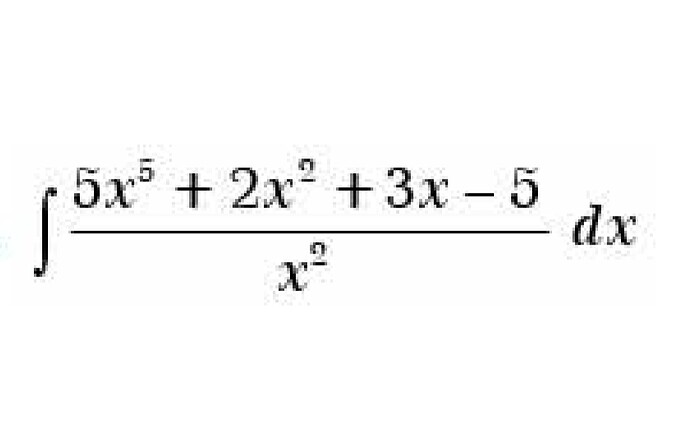Я не знаю как ее решить? Можете помочь?
Просто перепиши начальную финкцию как:
\frac{5x^5}{x^2}+ \frac{2x^2}{x^2}+ \frac{3x}{x^2}-\frac{5}{x^2}
2 лайка
А дальше уже изи
1 лайк
Хорошо, щас
У меня тут появился вопрос:
Почему
\int\limit\frac{5}{x^2} dx = \frac{5}{x}
Зная что:
\int (f(x)+g(x)) dx=\int f(x)dx+\int g(x)dx
Перепишем интеграл следующим образом:
I=\int \frac{5x^5}{x^2}dx+\int \frac{2x^2}{x^2}dx+\int \frac{3x}{x^2}dx-\int \frac{5}{x^2}dx
Сократим иксы:
I=\int5x^3dx+ \int2dx+ \int3x^{-1}dx-\int5x^{-2}dx
Далее по power rule мы знаем что:
\int x^ndx=\frac{x^{n+1}}{n+1}+C
Применяя это к каждому из них получаем:
I=\frac{5}{4}x^4+2x+3ln |x|+\frac{5}{x}+C
2 лайка
Хорошо, спасибо.
1 лайк