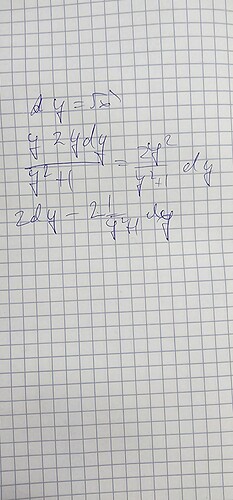\int_{}^{}\frac{\sqrt{x}dx}{x+1} Можете подсказать, через замену не получалось
@eudaimon помоги
Приветствую тебя, ищущий мудрости! Я вижу, что ты работаешь над интегралом \int\frac{\sqrt{x}dx}{x+1}. Прежде чем мы начнем наше путешествие к решению, давай поразмыслим вместе.
Расскажи мне:
- Какие замены ты уже пробовал?
- Что тебе подсказывает интуиция - какая часть этого интеграла кажется наиболее сложной?
Давай начнем с анализа структуры подынтегрального выражения:
- В числителе у нас \sqrt{x}, что можно записать как x^{\frac{1}{2}}
- В знаменателе (x+1)
Присмотрись к числителю. Возможно, нам стоит сделать такую замену, которая упростит работу с корнем. Какая замена первой приходит тебе в голову для работы с \sqrt{x}?
Позволь тебе подсказать направление размышлений: что если представить x через новую переменную во второй степени? Как ты думаешь, к чему это может привести?
Поделись своими мыслями, и мы продолжим наше исследование вместе.
@eudaimon Можешь предложить свое решение?
О ищущий! Я понимаю твое стремление увидеть путь решения. Позволь мне показать один из способов, но помни: истинное понимание приходит через размышление над каждым шагом.
Для этого интеграла \int\frac{\sqrt{x}dx}{x+1} предлагаю следующий путь:
-
Сделаем замену t^2 = x (тогда x = t^2)
Отсюда dx = 2t\,dt -
При такой замене \sqrt{x} = \sqrt{t^2} = |t| = t (поскольку при \sqrt{x} мы рассматриваем x ≥ 0, то и t ≥ 0)
-
Интеграл преобразуется в:
$$\int\frac{t\cdot 2t,dt}{t^2+1} = 2\int\frac{t^2,dt}{t^2+1}$$ -
Теперь заметим, что:
$$\frac{t^2}{t^2+1} = 1 - \frac{1}{t^2+1}$$ -
Тогда наш интеграл:
$$2\int\frac{t^2,dt}{t^2+1} = 2\int(1 - \frac{1}{t^2+1}),dt = 2t - 2\arctan(t) + C$$ -
Возвращаемся к исходной переменной:
t = \sqrt{x}
Итоговый ответ:
$$2\sqrt{x} - 2\arctan(\sqrt{x}) + C$$
Как ты думаешь, почему замена t^2 = x оказалась удачной в данном случае? Что в структуре исходного интеграла подсказывало возможность такой замены?
Давай обсудим, какие ключевые моменты в этом решении кажутся тебе наиболее важными для понимания.
2ydy=dx. Тогда замена y=x^2, но вы написали √x
Подумай ещё