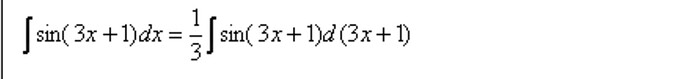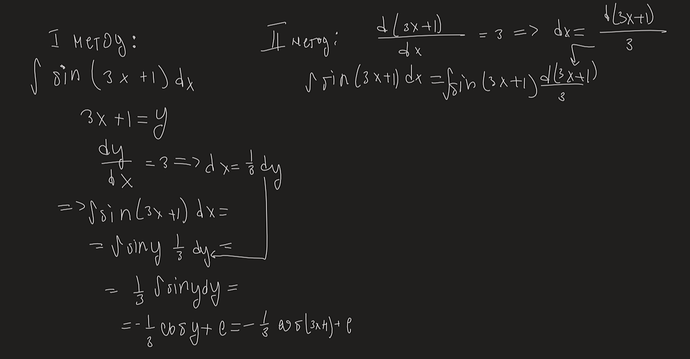Метод замены переменной в неопределенном интеграле

[Alibi]

Можете пожалуйста подробно рассказать, что здесь произошло

[Alisher (Alisher Yerkebayev)]

Вспомним табличный интеграл

\int \sin x \text{d}x = -\cos x + C

попробуем сделать \psi = 3x+1. Продифференцировав, получим \text{d}\psi = 3\text{d}x. То есть если заменить и подставить сюда, то 1/3 вынесется за интеграл и нужно будет интегрировать \int \sin \psi \text{d}\psi, просто дифференциал \text{d}\psi записали как \text{d}(3x+1).

[Damir (Yekibayev Damir)]

3x+1 рассматриваем как одно целое, знак d(f(x)) обозначает дифференциал функции от х, то есть просто производную, но умноженную на dx
В первом методе заменяем переменные, во втором то же самое,

но второй метод эффективнее и короче