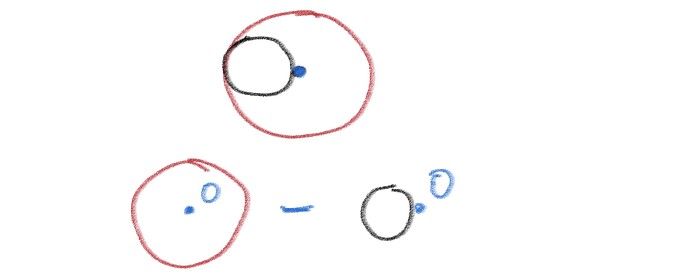
Однородный диск радиуса R имеет круг
лый вырез (рис. 1.53). Масса оставшейся (заштри
хованной) части диска равна m. Найти момент
инерции такого диска относительно оси, перпендикулярной плоскости диска и проходящей:
а) через точку O;
б) через его центр масс.
Как можно это решить, я многое испробовал и у меня не вышло,а также посмотрел решение через Задача по физике - 3578 | Образовательный портал. Решение задач по физике, математике, химии. Справочник физико-химических величин. Онлайн-учебники. и непонял что они сделали под конец.Я сделал так:
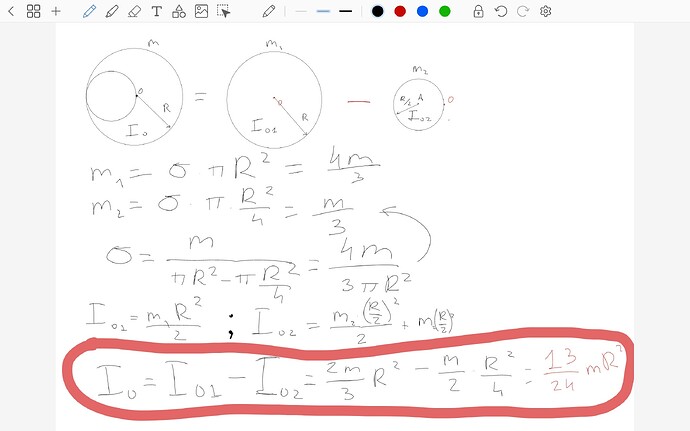
Чтобы найти момент инерций диска с дыркой,я минусанул момент инерций дырки от целого диска,но чето не вышло:
1 лайк
Ты че то замудрил с I_2, а в целом идея хорошая
Здесь I_{02} это момент инерции плоского диска с радиусом в два раза меньше первой относительно точки О, которую находим по теореме штейнера:I_{02}=m_2R^2/2+m_2\cdot^2(R/2)^2
Второй пункт тоже решается по теореме штейнера и суперпозицией, находишь положение диска с вырезом относительно точки О:
-m_2\cdot R/2=mx_{oc},
и дальше
I_0=I_C+m \cdot x_{oc}^2
3 лайка
Так в натури легче, спасибо
3 лайка