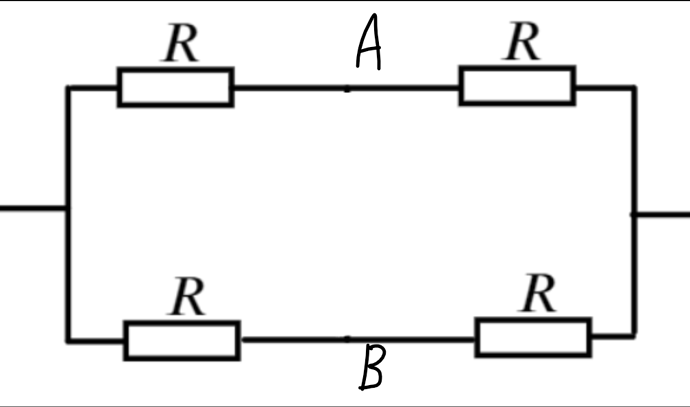
Подробное решение задачи
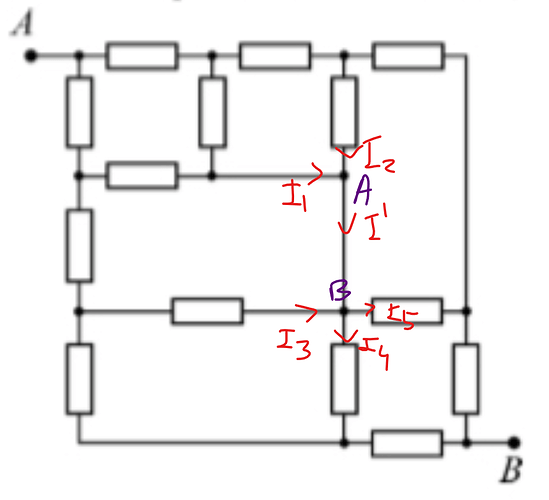
Для большей наглядности я соединю два узла, между которыми нет сопротивления, от этого схема не изменится.
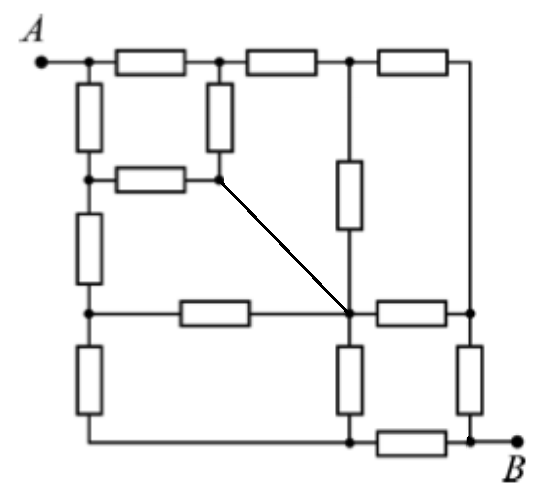
Как видно, вся схема симметрична вдоль диагонали AB, значит все симметричные относительно этой диагонали узлы имеют одинаковый потенциал. Это сводится к тому, что всю цепь можно “сложить пополам”, причём все (в данном случае все, так как на самой диагонали ничего нет) резисторы уже будут иметь сопротивление не R, а R/2. Выглядит это теперь так

Верхний вертикальный резистор не вносит никакого вклада в общее сопротивление, так как он является частью сбалансированного мостика. Мостик после свёртки будет иметь сопротивление R/2 и так как в конце остаются три таких последовательных сопротивления, то
Я не до конца понял как в последней части осталось лишь 3 резистора,можно этот момент по подробней?

Если перерисовать обведённую красным область, то получится такая вот эквивалентная цепь
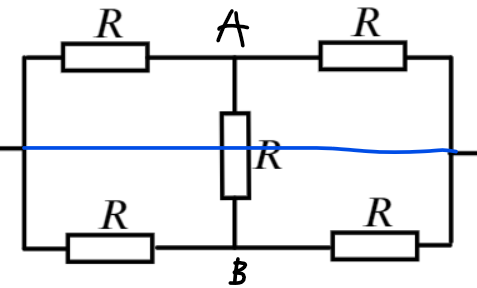
Она симметрично относительно синей линии, значит потенциалы в точках А и В равны. Значит мы можем стереть резистор посередине
А сопротивление данного участка найти очень просто, и оно равно R, только в этой задаче оно равно \frac R2, так как мы сложили изначальную цепь, как написал @Alisher
Можно ещё проверить правильность, если найти разность потенциалов между А и В, которая равна нулю, и сказать: \Delta \varphi _{AB}= 0 \Rightarrow добавление резистора ничего не изменит
Аа понял,большое спасибо
Какая-то чёрная магия
А почему? Разве они не соединены друг с другом косвенно через кучу резисторов, а соединяя напрямую мы даём току возможность идти иначе?
Если я правильно помню из школы, то если записать систему уравнений по законам Кирхгофа, то добавление еще одного соединения между точек с одинаковым потенциалом к схеме, равносильно добавлению в систему уравнения, которое линейно зависит от остальных и поэтому не влияет на решение.
То, что сказал @Sammael правильно, только в данном случае мы скорее убираем соединение между узлами А и В, тем самым уменьшая количество уравнений на одно, так как надобность в I' отпадает
В принципе того же самого эффекта можно достичь, если выразить I' через I_1 и I_2, а потом подставив в закон Кирхгофа для узла В.
ну точнее от нулевой разности потенциалов резистору становится ни холодно, ни жарко, можно безболезненно как добавлять контакт между узлами, так и убирать его