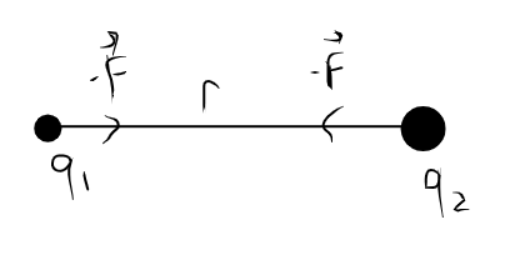
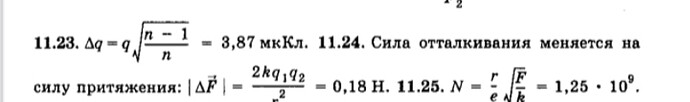Модуль силы не меняется, как был F = \frac {kq_1q_2}{r^2}, так и остаётся. Но меняется направление.
В первом случае так:
А во втором так
И если найти разность сил до и после, то мы получим значение силы в 2|F| = 2\frac {kq_1q_2}{r^2}
2 лайка
Если их силы равны,то разность не будеть равна нулю? Можно этот момент подробней
Пока отойдём от задачи рассмотрим разность векторов в общем случае.
Вот у нас есть вектора \vec {a} и \vec b. Чтобы найти \vec a - \vec b мы должны их нарисовать исходящими от одной точки и построить вектор от конца b до начала a
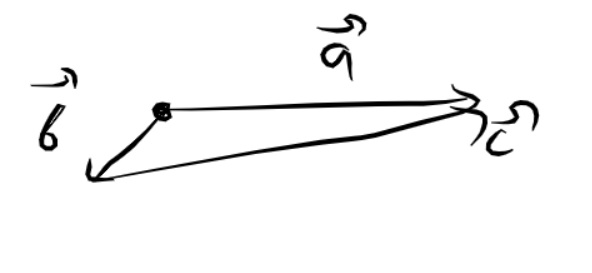
Как это выводится:
\vec c = \vec a - \vec b \\
\vec a = \vec b + \vec c
Другими словами, мы просто строим \vec a как сумму \vec b и \vec c.
Теперь посмотрим на заряд. На него действовала сила сначала \vec F, а потом сила - \vec F (такая же по модулю, но противоположная по направлению).
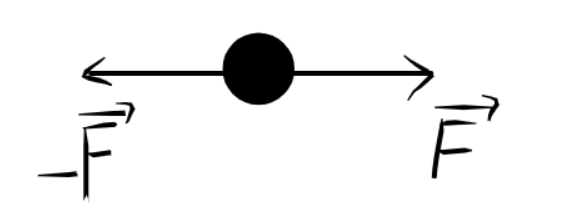
И мы просто находим разность этих сил, что у нас есть
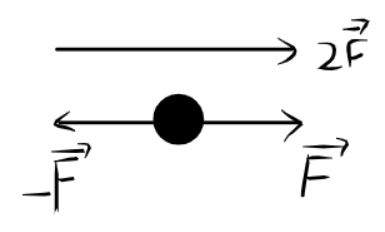
Или находя модуль разности |2F|
Ещё к этому можно прийти расписывая силы через координаты
"Метод через координаты
Направим ось х вправо:
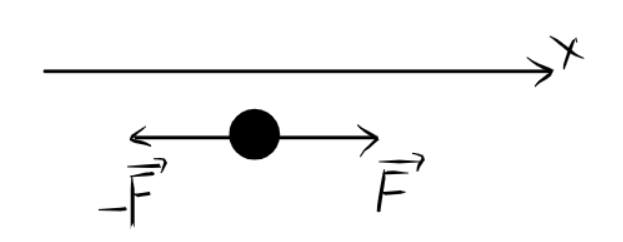
Тогда вдоль оси х на заряд сначала действует сначала сила F_x = F,а потом F'_x = -F, и находим разность F_x - F'_x = 2F.
Я так полагаю, что в решении они берут модуль дабы избежать путаницы с направлениями и знаками
4 лайка
Ааа,понял,спасибо
