2.26. Две скрещивающиеся взаимно перпендикулярные нити бесконечной длины заряжены равномерно с линейной плотностью λ. Найти силу их взаимодействия.
@28128 пишите пожалуйста предложения из задачи, а не несколько слов связанных с задачей
2 лайка
По теореме Гаусса находишь конфигурацию поля бесконечно заряженной нити. Находишь перпендикулярную проекцию элементарной силы, действующей на кусочек другой нити, интегрируешь.
P.S.
\int^{+\infty}_{-\infty}\frac{hdx}{h^2+x^2}=\int^{+\infty}_{-\infty}\frac{\displaystyle d\left(\frac{x}{h}\right)}{\displaystyle 1+\frac{x^2}{h^2}}=\arctan\frac{x}{h}\Bigg|^{+\infty}_{-\infty} = \frac{\pi}{2}-\left(-\frac{\pi}{2}\right)=\pi.
8 лайков
А почему поле нити у вас зависит как r^(-2)?
Нет. Квадратичная зависимость получается из-за того, что ещё нужно искать перпендикулярную проекцию силы для расчёта общего взаимодействия.
Да, согласен.
Хотя в общем для решения достаточно закона Кулона.
почему здесь именно перпендикулярная проекция к нити? Как раз таки в силу симметрии остается ведь лишь проекция вдоль нити, но считая и подставляя численные значения у меня выходит Е в проекции вдоль нити равным нулю, чисто визуально не могу принять этот факт, можете доказать пожалуйста
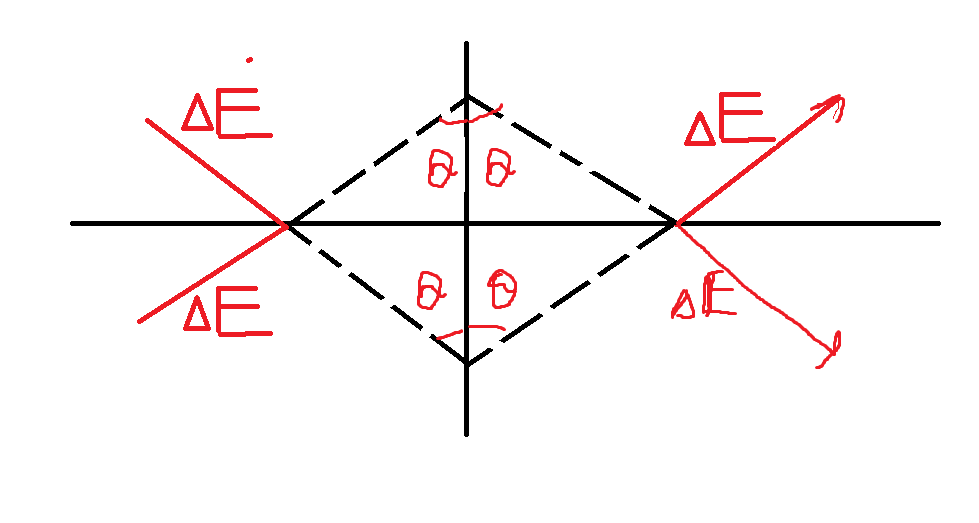
Представь картину, в которой одна нить лежит в плоскости рисунка, а вторая – перпендикулярно. В этой перспективе электрическое поле от перпендикулярной нити будет радиально расходиться из него. Если ты возьмёшь радиус-вектор \vec r от центра перпендикулярной нити к любой точке второй нити, и отмеришь угол \theta от ближашего расстояния между ними к \vec r, то всегда найдётся симметричная точка на углу -\theta, сила взаимодействия которой с перпендикулярной нитью будет противоположна той на +\theta в проекции на саму вторую нить. Только перпендикулярная проекция и остаётся нескомпенсированной. То, что ты получаешь в параллельной проекции 0 и было правильным, и никаких противоречий нет.
Можешь ли ты быть уверен в том, что правильно выразил направление вектора \vec E?
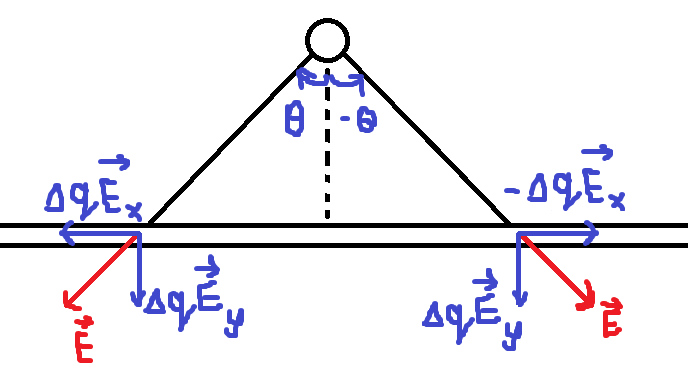
Вот так выглядит то, о чём я сейчас говорю
мне кажется что я неверно понимал смысл скрещивающихся мне казалось это те что пересекаются, а потом я с умным лицом пытался интегрировать и получить Е
Чисто чтобы удостоверится здесь же нити не пересекаются?
Да, не пересекаются. Твой рисунок верный, если это вид сверху, откуда не видно, что расстояние между «сходящимися» точками h (поэтому я и привёл этот параметр в подсказке с интегралом выше)
1 лайк
Спасибо!