Сама задача:
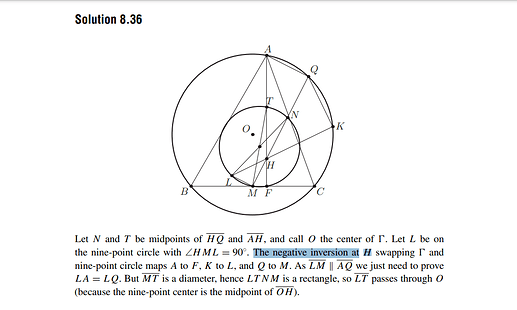
Let ABC be an acute triangle with AB > AC. Let Γ be its circumcircle, H its orthocenter, and
F the foot of the altitude from A. Let M be the midpoint of BC. Let Q be the point on Γ such
that ∠HQA = 90◦ and let K be the point on Γ such that ∠HKQ = 90◦
. Assume that the points
A, B, C, K and Q are all different and lie on Γ in this order. Prove that the circumcircles of
triangles KQH and FKM are tangent to each other.
Negative inversion - инверсия + симметрия относительно центра окружности симметрии.
Свойства те же самые, что и у обычной
-
Почему тогда просто не написать о том, что это преобразование - это инверся + симметрия?
-
И получается что таким образом можно концентрические окружности друг в друга переводить?
1.Ну тут ситуация схожа с “spiral similarity”, можно же ведь просто написать гомотетия + поворот, так что скорее всего просто для удобства
2.Можно, например если их центры находятся в центре окружности инверсии.
Хотя в данном решении друг в друга переводятся не концентрические у них центры разные O_9 и O