Как можно доказать, что у треугольника с центроидом G
\vec{AG} + \vec{BG} + \vec{CG} = 0?
Во-первых нужно понять, что если A_{1} , B_{1}, C_{1} - середины сторон противоположных сторон, то
\vec{AG} = \frac{2}{3}\vec{AA_{1}}, \vec{BG} = \frac{2}{3}\vec{BB_{1}}, \vec{CG} = \frac{2}{3}\vec{CC_{1}}, это основано на факте, что центроид делит медианы в отношении 2/1, считая от вершины, тогда доказать что
\vec{AG} + \vec{BG} + \vec{CG} = \vec{0} \iff
\frac{2}{3}(\vec{AA_{1}} + \vec{BB_{1}}+ \vec{CC_{1}}) = \vec{0} \iff \vec{AA_{1}} + \vec{BB_{1}}+ \vec{CC_{1}} = \vec{0}. Доказать надо это
Теперь нужно понять, что \vec{AA_{1}} = \frac{1}{2}(\vec{AB} + \vec{AC}) (аналогично для других векторов)
Из треугольника ABA_{1} \implies \vec{AA_{1}} = \vec{AB} + \vec{BA_{1}}
Из треугольника ACA_{1} \implies \vec{AA_{1}} = \vec{AC} + \vec{CA_{1}}
Суммирую равенства получаем:
2\vec{AA_{1}} = (\vec{AB} + \vec{AC}) + (\vec{BA_{1}} + \vec{CA_{1}}), теперь заметим что \vec{BA_{1}} = -\vec{CA_{1}}(Они равны по модулю и противоположно направлены)
Следовательно 2\vec{AA_{1}} = (\vec{AB} + \vec{AC}) \iff \vec{AA_{1}} = \frac{1}{2}(\vec{AB} + \vec{AC})
Тогда просумировав все такие равенства получим
\vec{AA_{1}} + \vec{BB_{1}} + \vec{CC_{1}} = \frac{1}{2}(\vec{AB} + \vec{AC} + \vec{BA} + \vec{BC} + \vec{CA} + \vec{CB}) =
\frac{1}{2}((\vec{AB} + \vec{BA}) + (\vec{BC} + \vec{CB}) + (\vec{CA} + \vec{AC})) = \frac{1}{2}(\vec{0} + \vec{0} + \vec{0}) = \vec{0}
Это же только для треугольника с одинаковыми сторонами?

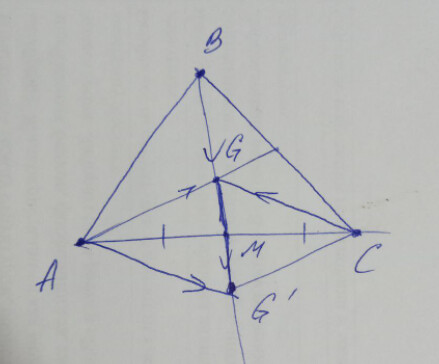
нет, рассмотри отдельно этот отрезок BC,
|BA_{1}| = |CA_{1}|, тогда \vec{u} + \vec{v} = \vec{0}
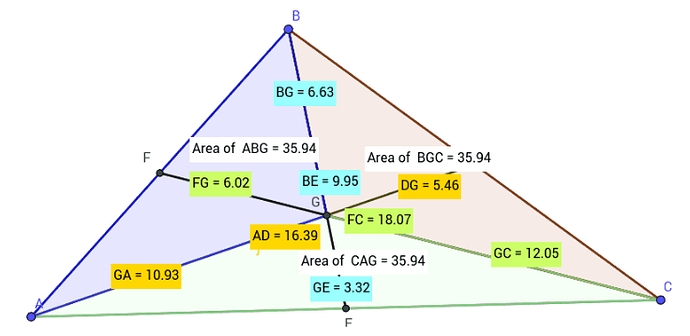
Длина у \vec{AF} и \vec{BF} одинаковые и они направлены противоположно к друг другу. Поэтому их можно сократить. Тогда получается, что \vec{GA} = \vec{GB}. По скриншоту видно, что это не так но я не понял почему
Их можно было бы сокатить, если б они были сонаправлены, а в этом случае сокращаются они если считать 2\vec{GF}=\vec{GA}+\vec{AF}+\vec{GB}+\vec{BF}, как и было показано в решении выше
Я только что посмотрел значение слово сонаправленные векторы и там написано, что это векторы с одинаковыми направлениями. Почему они сокращаются если при рисовании выходит сумма их длин?
Разве не всегда так?
Вот в этом уравнении они сокращаются)
Ой, я даун. Понял
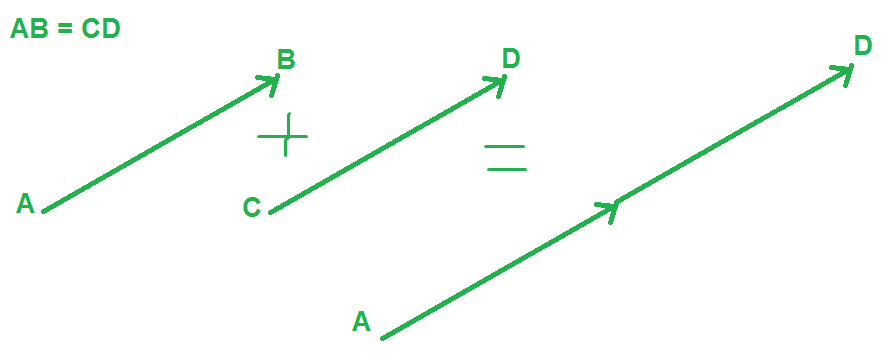
Используем идею переноса вектора (a.k.a. построение его из другой точки), которую преподают в школьной программе. Построем из точки GG' вектор, равный \vec{BG}. Тогда \vec{AG} + \vec{BG} = \vec{AG} + \vec{GG'} = \vec{AG'}.
Тогда осталось доказать, что \vec{AG'} = - \vec{CG}, но это означало бы, что AGCG' - параллелограмм. Тогда достаточно доказать, что AGCG' - параллелограмм.
Пусть M - середина AC. Зная, что медианы делятся в отношение 2:1, понимаем, что GM = \frac{BG}{2} = \frac{GG'}{2} = MG'.
Значит GM = MG', AM = AC, а потому AGCG' - параллелограмм.