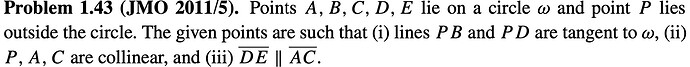Дошел до факта, что пересечение ЕС и АД это центр окружности. Обозначил очень много углов и еще пришел к тому, что (ii) ОВРД -впис, (iii) АО и ВО касательные окружности треугольника АВМ, где М точка пересечения ЕВ и АС. Мне нужно доказать, что ОМ перпендикулярно АС, однако в один момент я заметил, что углы ОАЕ и ОЕА у меня не равны(хотя должны быть такими) В чем моя ошибка?
1 лайк
Это не правда. Чтобы пересечение двух параллельных хорд совпало с центром окружности, необходимо, чтобы эти две хорды были равны. И в чем задача? Что надо доказать?
К слову OM не перпендикулярен AC.
1 лайк
Прошу прощения, зря быканул. OM действительно перпендикулярен AC.
Подсказка: если докажем, что M лежит на описанной BPD, то окажется, что \angle OMP = \angle ODP = 90^{\circ}. Последнее можно сделать уголками (ориентированными!).
3 лайка