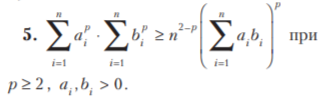Неравенство из статьи Кванта по неравенству Йенсена, нужна подсказка
Если p в условии натуральное, то можно решить так.
Для начала познакомимся с обобщенной формой неравенства Гёлдера.
Пусть \{a_i\}_{i=1}^{n}, \{b_i\}_{i=1}^{n}, \dots, \{z_i\}_{i=1}^{n} – какие-то k наборов положительных чисел. И пусть p_1, p_2, \dots, p_k – положительные числа такие, что \sum_{i=1}^{k}\frac{1}{p_i}=1. Тогда справедливо неравенство
\sum_{i=1}^{n}a_ib_i\cdots z_i \le \left(\sum_{i=1}^{n}a_i^{p_1}\right)^{\frac{1}{p_1}} \left(\sum_{i=1}^{n}b_i^{p_2}\right)^{\frac{1}{p_2}} \cdots \left(\sum_{i=1}^{n}z_i^{p_k}\right)^{\frac{1}{p_k}}.
Если в этом неравенстве заменить все p_i и k на p, а все p-2 наборов помимо \{a_i\} и \{b_i\} на наборы состоящие из n единичек, то получим
\sum_{i=1}^{n}a_ib_i\cdot \underbrace{1\cdots 1}_{p-2} \le \left(\sum_{i=1}^{n}a_i^{p}\right)^{\frac{1}{p}} \left(\sum_{i=1}^{n}b_i^{p}\right)^{\frac{1}{p}} \underbrace{\left(\sum_{i=1}^{n}1^{p}\right)^{\frac{1}{p}} \cdots \left(\sum_{i=1}^{n}1^{p}\right)^{\frac{1}{p}}}_{p-2} \iff
\sum_{i=1}^{n}a_ib_i \le \left(\sum_{i=1}^{n}a_i^{p}\right)^{\frac{1}{p}} \left(\sum_{i=1}^{n}b_i^{p}\right)^{\frac{1}{p}} n^{\frac{p-2}{p}} \iff \left(\sum_{i=1}^{n}a_i^{p}\right) \left(\sum_{i=1}^{n}b_i^{p}\right) \ge n^{2-p} \left(\sum_{i=1}^{n}a_ib_i\right)^p.
Надеюсь кто-нить ниже скинет решение через Йенсена 
4 лайка
Туф! Оказалось легче чем я думал 
По КБШ имеем, что \sum_{i=1}^{n}a_i^{p} \cdot \sum_{i=1}^{n}b_i^{p} \ge \left(\sum_{i=1}^{n} (a_ib_i)^{\frac{p}{2}} \right)^2. Тогда нам достаточно доказать, что
\left(\sum_{i=1}^{n} (a_ib_i)^{\frac{p}{2}} \right)^2 \ge n^{2-p}\left(\sum_{i=1}^{n}a_ib_i\right)^p \iff \frac{\sum_{i=1}^{n} (a_ib_i)^{\frac{p}{2}}}{n} \ge
\left(\frac{\sum_{i=1}^{n}a_ib_i}{n}\right)^{\frac{p}{2}},
что верно по неравенству Йенсена для выпуклой функции f(x)=x^{\frac{p}{2}}.
4 лайка