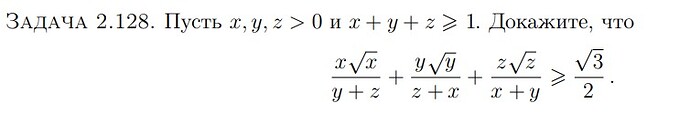Раздел по неравенству Йенсена. Можете подсказать как решать?
заметь что, если x + y + z \geq 1 \implies \frac 1 {\sqrt{x+y+z}} \leq 1
то есть ты можешь левую часть неравенства домножить на \frac 1 {x+y+z} и получить однородую штуку, отсюда подумай что дальше можно сделать
Что за книга?
mathus ru доказательство неравенств
Я домножил все на 1/sqrt(x+y+z) и получил слева степень 1. Можно ли теперь считать что x+y+z = 1? Если да, то тогда по неравенству Йенсена решается, иначе - не очень.
действительно, можно, так как теперь выражение слева - однородно (степень всего выражения равна 0, при этом степени всех “мономов” равны между собой)
допустим что a + b + c = s заменим a=a_1*s, b = b_1*s, c = c_1*s теперь подставь это и убедись что выражение слева фактически не поменялось, но при этом теперь a_1 + b_1 + c_1 = 1