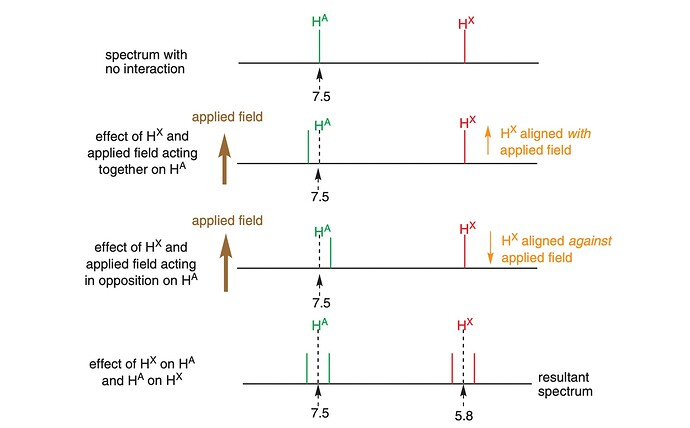
Как можно объяснить то, что когда спин H^{X} согласуется с примененным полем, химический сдвиг H^{A} повышается , а когда спин H^{X} противостоит примененному полю, химический сдвиг H^{A} уменьшается ? В книжке сказано, что в первом случае H^{A} испытывает примененное магнитное поле + локальное поле H^{X} , а во втором случае H^{A} испытывает примененное магнитное поле - локальное поле H^{X} . Так вот, я не могу понять причину того, почему суммиировали и отняли локальное поле
1 лайк
Я понимаю ЯМР так: мы создаем внешнее магнитное поле. Из-за этого у ядер \ce{^1H} и \ce{^{13}C} появляются два состояния — в одном состоянии они повернуты так, что индуцированное ими магнитное поле направлено в ту же сторону, что и внешнее, во втором они повернуты так, что их магнитное поле направлено противоположно к внешнему. И в первом случае энергия ниже. Это означает, что при каком-то определенном излучении энергии ядра могут перейти из этого в состояния во второе — с более высокой энергией, и мы смотрим на то, при каких частотах волн происходит этот переход.
Чем выше сила магнитного поля, тем больше разница в энергии между этими двумя состояниями, и, соответственно, больше разница в частоте и в химическом сдвиге.
У \ce{H^X} есть такое же магнитное поле, как и у \ce{H^A}. И оно так же может либо совпадать по направлению с внешним полем либо иметь противоположное направление. Если оно ориентировано противоположно, то оно будет противодействовать внешнему магнитному полю и таким образом его немного ослаблять. Если же оно будет ориентировано вместе с внешним полем, оно будет, наоборот, делать его более сильным. И тогда будет два варианта для перехода \ce{H^A}: в поле, которое чуть более сильное и в поле, которое чуть более слабое. Как мы сказали ранее, от этого зависит разница в энергии состояний, поэтому в итоге у нас два варианта для энергии перехода — один чуть больше по энергии, другой чуть меньше.
5 лайков
Я кстати так и не понял почему когда индуцированное ими магнитное поле направлено в ту же сторону, что и внешнее энергия будет ниже. Я как то попробовал привести аналогию с отталкиванием однозарядных ионов, из-за которого повышается энергия. Только в этом случае происходит что-то наподобие “отталкивания” спинов, но честно говоря, не знаю насколько правильна эта мысль, мб у тебя будут какие то идеи насчет этого (?)
Я правильно понимаю, что когда индуцированное магнитное поле H^{X} противодействует внешнему магнитному полю, это приводит к ослаблению внешнего магнитного поля, и поскольку H^{A} находится достаточно близко к H_{X} , то ослабление внешнего магнитного поля коснется и H^{A} ?
Да, для него это будет как бы новым внешним полем. И из-за того, что от силы поля зависит энергия перехода, получатся два разных сдвига.
Вообще, этот вопрос меня тоже довольно долго мучает. Все никак не могу прийти к какому-то адекватному объяснению. У меня в целом есть пробелы в понимании электричества и магнетизма, и я не понимаю, например, почему более сильное поле увеличивает разницу в энергиях. Я попробую поискать ответ и надеюсь не позже вторника найду его и поделюсь.
Вам сюда:
И сюда
UPD: можно еще сюда
4 лайка
А теперь поясню эту штуку со стороны физики)
Вообще, теория магнетизма строилась на основе экспериментов с исследованием магнитных полей от проводов с током, так что сначала отвлечёмся от природы возникновения магнитного поля и затем распространим результаты вычислений на атомы. Ещё добавлю то, что некоторые уравнения выводились таким образом, чтобы было аналогичное сходство с явлениями в электростатике.
Здесь нас интересует круговой виток с током. Контур этого витка, вообще, может быть произвольным, но сначала для простоты примем, что этот контур прямоугольный.
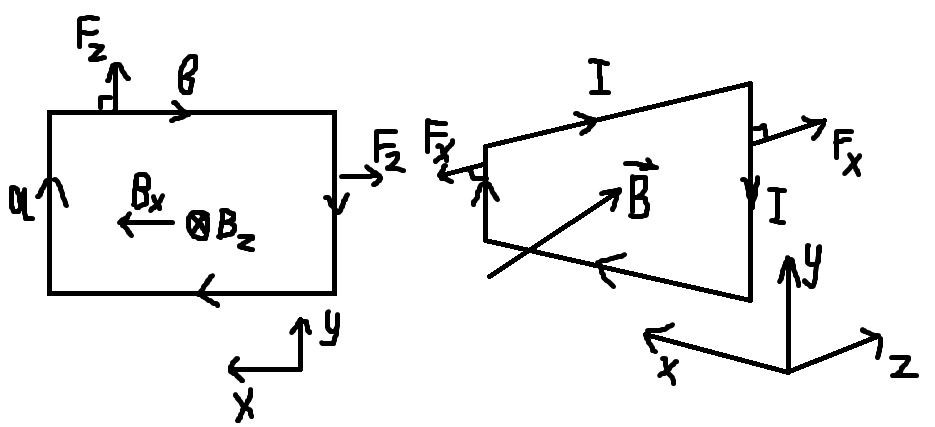
Пусть этот прямоугольный виток лежит в плоскости xy. Если приложить к нему однородное поле с компонентами B_x, B_z (для простоты пусть B_y=0), то на виток начинает действовать сила Ампера. Для тех, кому лень открывать ссылку, процитирую:
Сила d\vec F, с которой магнитное поле действует на элемент d\vec l проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины d\vec l проводника на магнитную индукцию \vec B
d\vec F = Id\vec l \times \vec B.
Посмотрим на действие сил на каждую сторону витка. Вспоминая школьное правило левой руки, можно определять направления этих сил. Как видно, компонента B_z, которая перпендикулярна контуру, действует на все стороны этого витка, растягивая его. Это не представляет нам никакого интереса.
Компонента B_x параллельна стороне контура длины b и поэтому не действует на неё. Но она перпендикулярна стороне a и её направление перпендикулярно плоскости витка. Её сила Ампера равна
F_x=B_x I a,
и за счёт пары этих сил на противоположные стороны образуется момент силы, стремящийся раскрутить этот виток относительно оси y через геометрический центр:
M_y = 2\cdot F_x \frac{b}{2}=B_xIab=B_xIS
Из-за векторного равенства нулю сил виток в целом неподвижен и просто стремится раскрутиться так, чтобы расположиться параллельно полю B_x.
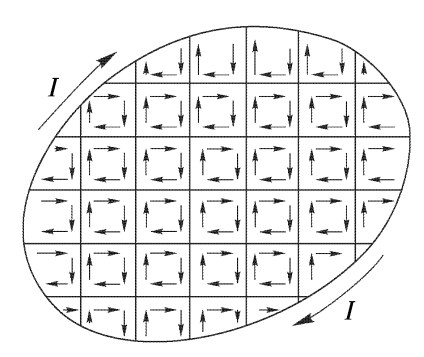
В электростатике электрический диполь в однородном электрическом поле ведёт себя аналогично. Так что в магнитном учении вводится магнитный диполь \vec m= I\vec S, здесь она направлена перпендикулярно контуру в правовинтовом направлении тока (по рисунку слева от нас). В случае произвольного витка с током достаточно его мысленно разделить на бесконечное множество малых прямоугольных контуров. Дипольные моменты этих прямоугольников складываются и дают общую площадь S, не зависящую от формы витка.
В общем случае магнитное поле прикладывает к диполю момент сил
\vec M = \vec m \times \vec B.
Что из себя представляет эта формула? Если угол между векторами \vec m и \vec B составляет \alpha, то по определению векторного произведения величина M равна mB\sin \alpha. Когда эти два вектора коллинеарны, то момент сил нулевой, и магнитный диполь находится в состоянии с минимальной потенциальной энергией. Это качественно объясняет этот вопрос:
Но если кому интересно, то вот вывод для потенциальной энергии:
Эта энергия появляется из-за способности моменту сил раскрутить виток и совершить тем самым работу. Элементарная работа dA получается при раскручивании на малый угол d\alpha. Запишем интеграл:
U = \int Md\alpha = \int mB\sin \alpha d\alpha = -mB\cos \alpha + C.
Таким образом, если магнитный момент направлен вдоль \vec B, то U=-mB + C, а если против, то U = mB + C. Как видим, в первом случае энергия минимальна, а во втором случае – максимальна, разность между ними равна \Delta U = 2mB. То есть, чем сильнее магнитная индукция, тем больше разница в энергии, что объясняет утверждение ниже.
Всё это объяснение было на основе классической теории, которая хорошо описывает магнитные явления классического атома, например, то, что орбитальное движение электрона по замкнутой траектории и порождает магнитный момент атома. В учении о магнетизме существенна не наглядность этого движения, более важны механический и магнитный моменты, связанные с этим движением, так что и переход на квантовую модель не отменяет всего вышесказанного.
13 лайков
Только ради этого твоего поста можно было создавать аск
6 лайков