Optimizing silo equation

Математика Школьная математика
1

A silo is to be made out of two pieces of material, one for the sides of the silo, and another for the
hemispherical dome that will go on top of the cylinder. The silo must be able to contain 2500 m3
of material. If the cost for the cylinder part is $150/m2 and the cost for the hemisphere is $225/m2, what dimensions for the silo will minimize the cost of construction?

где я ошибся?

чтобы

найти

самый минимальную цену, я совместил 2 функции.

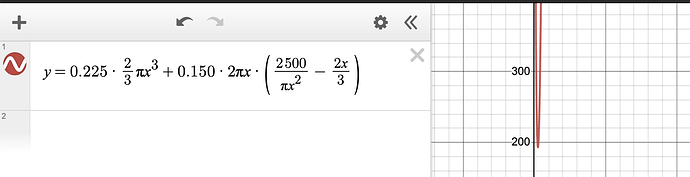
  • Cost=150(2πrh)+225(2πr^2)=2πr(150h+225r)
  • 2500=Vcyl+Vhem=πr^2+2/3πr^3=πr^2(h+2/3r)

после выразил h в функции с обьемом:

  • h=2500/πr^2-2/3r

финальная функция:

  • Cost=150(2πr(2500/πr^2-2/3r))+225(2πr^2)=2πr(150h+225r)

Cost=f(x), r=x

image
image542×956 28.2 KB

как получить правиьную фукнцию?

2

Концептуально все верно, ошибка заключается лишь в выражении для h.

2500 = \pi r^2h + \frac{2\pi r^3}{3} ; \ h = \frac{2500-\frac{2\pi r^3}{3}}{\pi r^2} = \frac{2500}{\pi r^2}-\frac{2r}{3}

У тебя радиус оказался в знаменателе, хотя он должен быть в числителе.

2 лайка
3

Вы указали мою ошибку, или Ваше решение?

4

@Madsoul указал вашу ошибку. Тут не 2/3r, а 2r/3

5

Загрузка: image.jpg…
Я исправил ошибку, но local minimumа нет

6

Ваш скрин не прикрепился:

image
image1726×444 42.9 KB

x=r