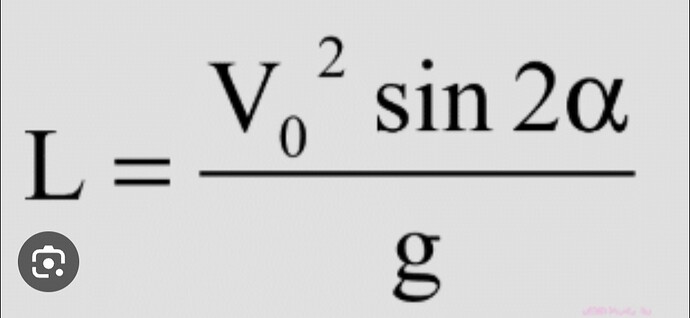Подскажите, пожалуйста, как мне найти угол между скоростью и крышой ангара в момент, когда мячик дошел до левой верхней вершины ангара.
1 лайк
недавно ведь ты создавал тему, в которой получил выражение за счет того что приравнял к нулю уравнение в корне, этим методом и решается данная задача
задачу можно решаить если тs рассмотришь только верхнюю часть ангара, логично что если у нас есть тело и мы хотим чтобы оно полетело максимально далеко нужно бросить по 45 градусов
зная угол (45 ) и длину нак которое полетит шари( L ) ты сможешь наити минимальную скорость у угла ангара (назовем V1). Потом через закон сохранения энергий находишь скорость у земли mVmin^2/2 = mgh + mV1^2/2
оттуда выражаешь Vmin и получаешь ответ
1 лайк
А почему максимально далеко?
максимальное значение длины полета достигается при a=45°, тогда синус получится равным единице, а при других значениях угла будет меньше нее и следовательно расстояние тоже
2 лайка
не, это я знаю, но почему в нашем случае стоит брать максимальную длину полета?
- нам же нужно пролететь L метров, если мы рассматриваем только крышу амбара, но это же не обязательно максимальная длина полета
якобы если ты наидешь минимальную скорость требуюмую для перелета ангара с верхнего края, то по закону сохранения энергий которое я писал выше видно что ты также наидешь и минимальную скорость бросания мячика с земли.
тоесть у тебя может быть любое значение Vn( скорость у края ангара).
По закону схорнанеия энергий дегко наити скорость у земли Vb.
m(Vb^2)/2 = mgh + m (Vn^2)/2
отсюда видно что минимальная скорость у земли достигается при минимальной скорости у края ангара, наидя ее получаешь ответ 
я нахожу именно у края ангара, нам же нужно наити минимальную скорость при которой она приодолеет L 
2 лайка
ААА, понял, спасибо
1 лайк
уряяяя 
2 лайка