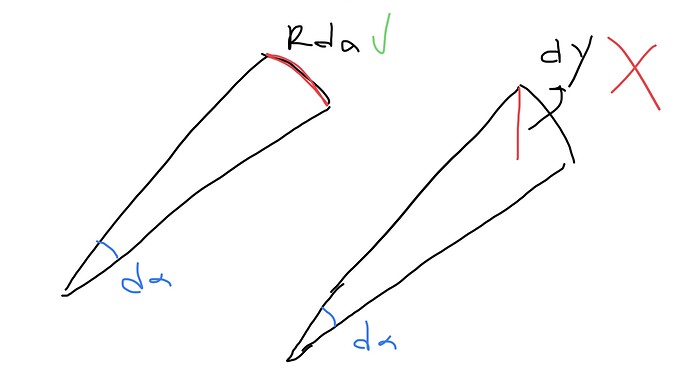
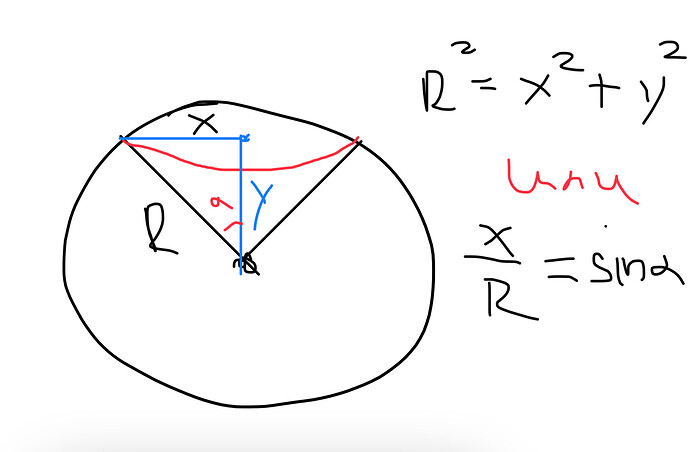Увидел задачу, с нахождением объема вращения графика функции вокруг Ox.
Впринципе, не сложно, и довольно быстро вывел формулу
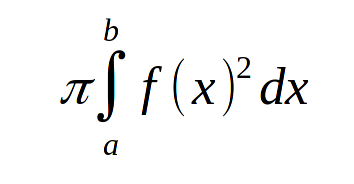
Просто поделив фигуру на составляющие цилиндры, у которых очевидно будет объем:
pic1
Но, на этом не остановился, и решил найти площадь поверхности.
Подумав, а почему бы просто как и в прошлый раз, не использовать разделение цилиндров и суммирование площадей (глупая, идея. Сразу приходили в голову идеи странной ступенчатости). Формула получилась вот-такой.
pic2
И что это в бесконечном приблежение будет давать объём.
Подумав, что это окончательная победа, я решил погуглить настоящие формулы, и тут оказалось, что вторая формула не верна.
В интернете причину, я не смог просто найти. И решил самостоятельно доказать.
Свёл это к нахождению двумерному случая, то есть длине кривой. Если использовать, немного преобразованую формулу повыше, для этого случая получается бред.
pic3
Что, понятно просто b - a. То есть вместо длины мы получаем проекцию на Ox.
Хорошо, понятно теперь, что надо считать через ломаную.
И получается в итоге формула площади поверхности равняется.
pic4
И теперь собсна вопрос, а как тогда находить такие функции, которую нашу функцию апроксимировала, и которая в бесконечно малых приблежениях равнялась ей.
P.S. Извините за терминологию, и некоторый бред в разнеснениях, мат. анализ знаю только по паре роликов от 3b1b, и небольшой информации с Википедии
Pic1:
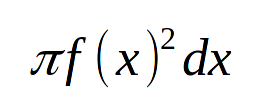
Pic2:
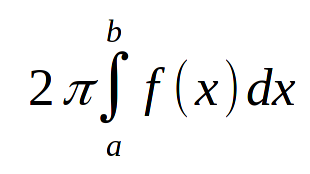
Pic3:
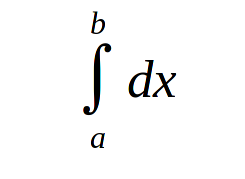
Pic4:
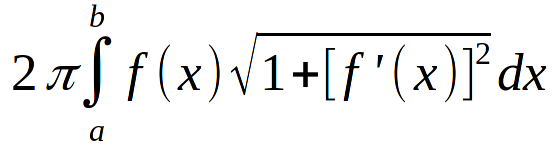
Прикол в том, что разделение цилиндрами не даст нам точного ответа из-за кривизны поверхности.
Для примера возьмём сферу. По твоему принципу площадь её поверхности:
Или же \int2 \pi \sqrt{(R^2-y^2)}dy . Из этого ничего толкого не выйдет.
А если теперь учесть кривизну то получим что:
Далее учитывая что x=Rsin\alpha получаем:
При интегрировании от -\frac{\pi}{2} до \frac{\pi}{2} получаем:
Твой принцип можно использовать только при \frac{df(x)}{dx} стремящейся нулю.
Тогда кривые будут подобны цилиндру.
@arman_dx Спасибо, а не можешь ли подсказать материал, для изучения этой темы.
Как писал выше, теоретическая часть крайне слаба. Буквально полплейлиста от 3b1b, лол.
Я тоже учил интегралы посмотрев полностью плейлист от 3b1b а дальше просто смотрел видосы из канала blackpenredpen. Книги по типу Томаса учил только поверхностно. Ещё есть канал integrals for you где я решал интегралы.
Ок, понял.
Можно по идее книгу про интегралы от замбака почалить. Там есть задачи на такие темы.
не совсем уверен, что это не подгониан. Все таки, если речь идет про сферу, по хорошему x=\sqrt{r^2-y^2-z^2}
@if2koa могу порекомендовать эти курсы:
Ибо в общем случае площадь – это двойной интеграл, а объем – тройной.
Для тел, обладающих цилиндрической и (или) сферической симметрией, можно переводить интеграл в цилиндрические и (или) полярные координаты соответственно (при этом, подынтегральное выражение будет содержать множитель Якоби