Помогите, пожалуйста, с задачей. Не знаю, что делать. В задаче ссылаются на картинку, но в пробнике ее не было, и я не понимаю, как выглядит эта фигура.
1 лайк
Фигура состоит из цилиндра и полусферы такого же радиуса. Радиус полусферы и цилиндра r , высота цилиндра l .
Чтобы найти объем всей фигуры, нужно сложить объемы составляющих её цилиндра и полусферы.
Объем полусферы — половина от объема сферы
V_1=\frac{1}{2} \cdot \frac{4}{3}\pi r^3 = \frac{2}{3} \pi r^3
Объем цилиндра
V_2=\pi r^2 l
Объем всей фигуры
V=V_1+V_2= \frac{2}{3} \pi r^3 + \pi r^2 l = \frac{\pi r^2}{3} \left( 2r + 3l \right)
6 лайков
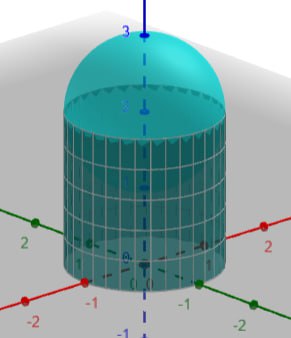
- вот схема данного задания
для того, чтобы определить всю площадь данной фигуры, нам понадобится две формулы: обьем цилиндра и обьем полусферы, так как они стоят вместе и радиусы у этих фигур идентичны.
тогда получается:
V=V_{cylinder} + V _{hemisphere}
нужно подставить сюда вольюм каждой фигуры
объем цилиндра: V_{cylinder} = \pi\cdot r^2l,
V_{hemisphere} = \displaystyle\frac{1}{2}\cdot V_{sphere} = \displaystyle \frac{1}{2}\cdot \frac{4}{3}\cdot \pi\cdot r^3 = \frac{2}{3}\cdot \pi r^3
*l это высота цилиндра, а r это радиус
тогда у нас получается следующее:
V= \pi\cdot r^2l + \displaystyle\frac{2}{3}\cdot \pi r^3
отсюда ответ будет:
V = \displaystyle\frac{\pi \cdot r^2}{3} \cdot (2r+3l)
6 лайков