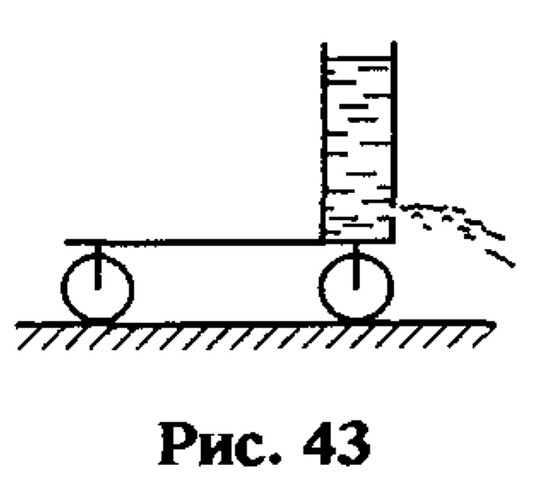
3.12. На краю массивной тележки (рис. 43), покоящейся на горизонтальной плоскости, укреплен цилиндрический сосуд радиуса r и высоты H, в нижней части которого имеется небольшое отверстие с пробкой. Сосуд наполнен жидкостью плотности р. В момент времени t = 0 пробку вынимают.Найти максимальную скорость, которую приобретает тележка, считая, что H>>r и M>>{\rho}r^2{\pi}H, где М масса тележки с сосудом. Пояснить смысл этих ограничений. Трением в подшипниках тележки, трением качения и внутренним трением жидкости пренебречь.
Как решить задачу