Как можно понять “можно/нельзя опрокинуть”. Хочется связать это с моментами сил относительно точки соприкосновений в качестве оси, чтобы силы нормальных давлений шариков об друг друга ушли
тебе нужно доказать/показать что моменты сил шариков сокращают друг друга.Грубо говоря,показать условия в котором шарики не перевернут этот цилиндр.Если в конце концов выйдет что моменты сил шариков не сокращают друг друга то его можно опрокинуть а если сумма моментов равна нуля то нельзя.
вырази tg через радиусы
Я как то решала эту задачу, и у многих тоже возникали вопросы по этой задаче, поэтому отвечу.
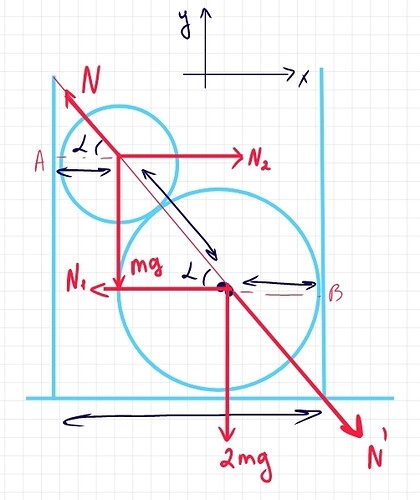
Напишем проекцию на оси х и у:
ox: N_2 = N \cdot cos\alpha;
oy: N = \dfrac{mg}{sin\alpha}
Отсюдого найдем: N_2 = mg\cdot ctg\alpha
Так как стенки цилиндра давят одинаково, то: N_1 = N_2
Теперь найдем угол \alpha:
У нас в цилиндре есть два максимальных расстояний. Это расстояние от А к В, и диаметр цилиндра, поэтому справедливо это равенство:
r + 3rcos\alpha + 2r = 2R
3r(1 + cos\alpha) = 2R
cos\alpha = \dfrac{2R}{3r} - 1
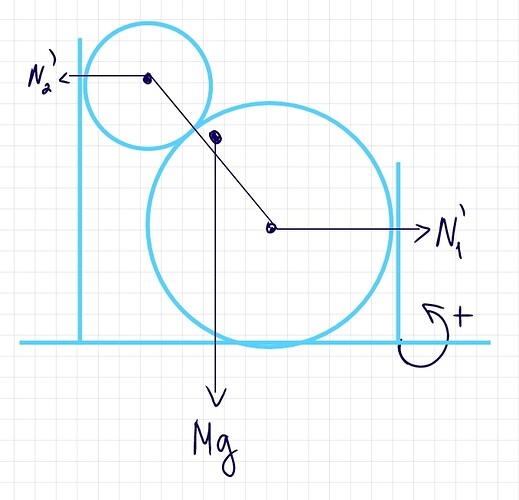
Теперь по второму рисунку, мы взяли общий вес цилиндра, и равнодействующие силы N_1 ={N_1}^* и N_2 ={N_2}^*
● N_1 = N_2 = mg \cdot ctg\alpha
У нас есть два момента сил, которые стремятся повернуть цилиндр в положительную сторону(против часовой), и одна сила которая стремится повернуть по часовой:
M^+ \in \{ N_1; Mg\}
M^- \in \{N_2\}
M_1 = N_1 \cdot 2r
M_2 = MgR
M_3 = N_2 (2r + 3rsin\alpha)
\sum M^+ = \sum M^-
Подставляем:
N_2 (2r + 3rsin\alpha) = N_1 \cdot 2r + MgR
2mr \dfrac{cos\alpha}{sin\alpha} + 3mrcos\alpha = 2mr\dfrac{cos\alpha}{sin\alpha} + MR
MR = 3mrcos\alpha = \dfrac{m(2R - 3r)}{R}
При M \geq \dfrac{m(2R-3r)}{R}, цилиндр не опрокинется; где М- это масса цилиндра.
Вы кстати так же можете тригонометрические функции писать через черточку:
$\sin x$ for \sin x
$\cos x$ for \cos x
$\tan x$ for \tan x
$\cot x$ for \cot x
$\ctg x$ for \ctg x
$\tg x$ for \tg x
2 лайка