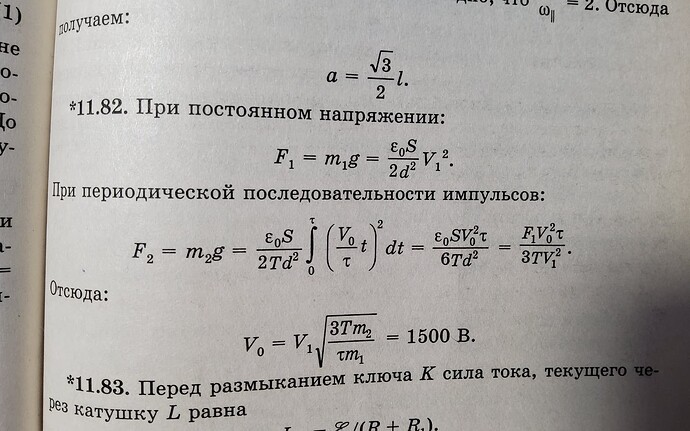В электростатическом вольтметре сила притяжения между металлическими пластинами плоского конденсатора C измеряется с помощью аналитических весов (рис. слева). При постоянном напряжении V1 = 500 В между пластинами 1 и 2 весы уравновешиваются разновесом массой m1 = 200 мг. На пластины конденсатора подаётся периодическая последовательность треугольных импульсов напряжения с длительностью τ =5·10−4 с и периодом повторения T = 0,01 с (рис. справа). Чему равна амплитуда импульсов V0, если в этом случае весы уравновешиваются разновесом массой m2 = 30 мг? Период собственных колебаний весов много больше T.
помогите разобраться что мы во второй формуле делаем
Сила притяжения между пластинами конденсатора F=\frac{\sigma ^2S}{2\varepsilon_0}=\frac{C^2V^2}{2\varepsilon_0 S}, для плоского воздушного конденсатора C=\frac{\varepsilon_0S}{d}, тогда выражение для силы F=\frac{\varepsilon_0SV^2}{2d^2}. Во втором случае, когда подаются треугольные импульсы, т.е. когда V(t)=\frac{V_0t}{\tau }, у нас напряжение непостоянно и чтобы найти силу нужно брать ее среднее значение. Учитывая то, что сила зависит только от напряжения
\langle F\rangle =\frac{\varepsilon_0S}{2d^2}\langle V^2\rangle=\frac{\varepsilon_0S}{2d^2}\left(\frac{1}T{}\int \limits_{t}^{t+T}V^2(t)dt\right)
Как видно из графика напряжение меняется только в интервале [t;t+\tau ], поэтому интеграл \int\limits_{t}^{t+T }V^2dt равен интегралу \int\limits_{t}^{t+\tau }V^2dt. Поэтому ср. знач. силы можно записать как
\langle F\rangle=\frac{\varepsilon_0S}{2d^2}\frac{1}T\int \limits_{t}^{t+\tau}V^2(t)dt
5 лайков