Распределение максвелла частота ударов о стенку матвеев

[Ayana123]

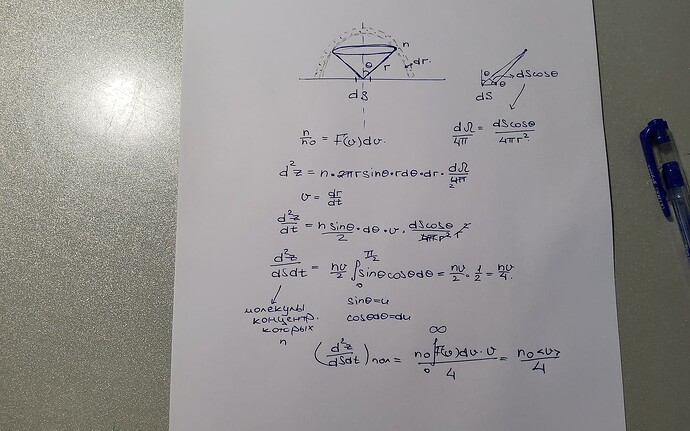
мне непонятен переход к тройному интегралу (8.32) или что это вообще, и сомневаюсь в выводе первой формулы:

(1): частота, N_{ст} - столкнувшиеся со стенкой

\frac{\nu}{S} = \frac{1}{S}\frac{dN_{ст}}{dt}

(2): вероятность обладания молекулой скоростью в [v, v+ dv], dN(v) - число молекул, обладающих этой скоростью, N - те, что близки к стенке

f(v)dv = \frac{dN(v)}{N}

N = n_0V = n_0Sv_xdt

dN(v) = Nf(v)dv = n_0Sv_xf(v)dvdt

(3): столкнутся со стенкой все, удовлетворяющие условию близости к ней (2)

dN_{ст} = \int_{по \space скоростям} dN(v) = n_0Sdt\int_{по \space скоростям} v_xf(v)dv

[Upward (Tair)]

[Ayana123]

все я понял, такой же трюк в обратн сторону при выводе использовался(
там в функции распр есть кусочек с 4\pi v^2, и складываются (...)^{3/2}\exp(...) по скоростным обьемам по сферам 4\pi v^2dv. Вместо этого перешли к dv_xdv_ydv_z, чтобы можно было пределы инт учесть