При интегрировании данного уравнения у меня получается 0. Как вышло =(3RT/m)’1/2? То есть, как его проинтегрировали так?
1 лайк
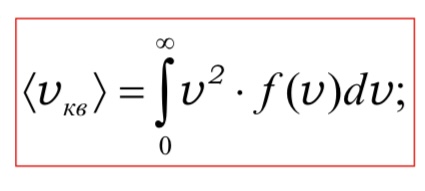
Эти темы могут быть полезными:
P.s Будет лучше если вы поделитесь с вашим решением.
5 лайков
Да, я просматривала данные темы и поняла откуда взялась эта формула через среднюю энергию. Но мне интересно как интегрируется именно это выражение, чтобы прийти к самой формуле скорости, поскольку у меня получается 0.
1 лайк
@stainless.steel не знаю как вы интегрировали, но хотел бы поделиться интересным методом нахождения значения интеграла (конечно можно посчитать в лоб, используя гамма функцию и т.д., но это долго и неэффективно)
\langle v^2\rangle =\int \limits_{0}^{\infin}\left(\frac{m}{2\pi kT}\right)^{3/2}4\pi v^4e^{-\frac{mv^2}{2kT}}dv=4\pi \left(\frac{m}{2\pi kT}\right)^{3/2}\int \limits_{0}^{\infin}v^4 e^{-\frac{-mv^2}{2kT}}dv
Нам нужно вычислить интеграл \int \limits_{0}^{\infin}v^4 e^{-\frac{-mv^2}{2kT}}dv и более удобно будет выразить этот интеграл как
\int \limits_{0}^{\infin}v^4 e^{-\frac{-mv^2}{2kT}}dv=\frac{1}{2}\int \limits_{-\infin}^{\infin}v^4 e^{-\frac{-mv^2}{2kT}}dv
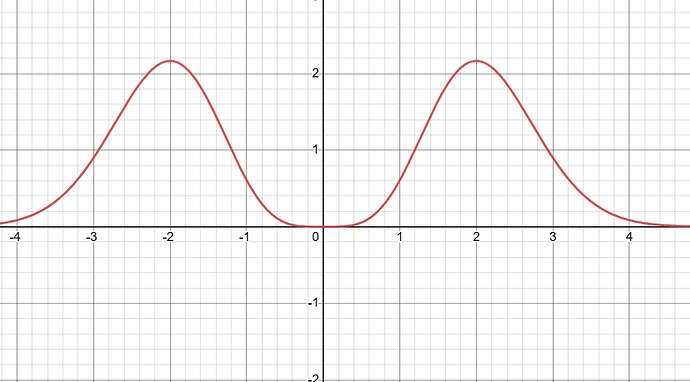
Так можно сделать, так как функция v^4 e^{-\frac{-mv^2}{2kT}} четная и симметричная, поэтому площадь под графиком в интервале [0;\infin] равна половине площади в интервале [-\infin;\infin]
Теперь найдем интеграл \int \limits_{-\infin}^{\infin}v^4 e^{-\frac{-mv^2}{2kT}}dv и потом разделим на два, чтобы найти интеграл \int \limits_{0}^{\infin}v^4 e^{-\frac{-mv^2}{2kT}}dv. Для этого нужно знать решение всего лишь одного простого интеграла
\int\limits_{-\infin}^{\infin}e^{-\alpha x^2}dx=\sqrt{\frac{\pi}{\alpha}}
Здесь у нас \alpha =\frac{m}{2kT}\quad v=x. Возьмем частную производную интеграла по коэффициенту \alpha:
\frac{\partial}{\partial \alpha}\left(\int\limits_{-\infin}^{\infin}e^{-\alpha x^2}dx\right)=-\int\limits_{-\infin}^{\infin}x^2e^{-\alpha x^2}dx
Теперь вторую частную производную по коэф. \alpha:
\frac{\partial^2}{\partial \alpha^2}\left(\int\limits_{-\infin}^{\infin}e^{-\alpha x^2}dx\right)=\int\limits_{-\infin}^{\infin}x^4e^{-\alpha x^2}dx
По сути интеграл \int\limits_{-\infin}^{\infin}e^{-\alpha x^2}dx это и есть \sqrt{\frac{\pi}{\alpha}}, поэтому частная производная этого интеграла по \alpha это и есть частная производная \sqrt{\frac{\pi}{\alpha}} по \alpha
\int\limits_{-\infin}^{\infin}x^4e^{-\alpha x^2}dx=\frac{\partial^2}{\partial \alpha^2}
\left(\sqrt{\frac{\pi}{\alpha}}\right)=\frac{3\sqrt{\pi}}{4\alpha^{5/2}}
В результате для интеграла скорости
\int\limits_{-\infin}^{\infin}v^4e^{-\frac{mv^2}{2kT}}dv=\frac{3\sqrt{\pi}}{4}\left(\frac{2kT}{m}\right)^{5/2}\rightarrow \int\limits_{0}^{\infin}v^4e^{-\frac{mv^2}{2kT}}dv=\frac{3\sqrt{\pi}}{8}\left(\frac{2kT}{m}\right)^{5/2}
Ну а дальше
\langle v^2\rangle=4\pi\left(\frac{m}{2\pi kT}\right)^{3/2}\left(\frac{3\sqrt{\pi}}{8}\left(\frac{2kT}{m}\right)^{5/2}\right)=\frac{3kT}{m}
Здесь просто нужно было знать интеграл \int\limits_{-\infin}^{\infin}e^{-\alpha x^2}dx=\sqrt{\frac{\pi}{\alpha}}, а все остальное это простые логические рассуждения
22 лайка
1 лайк
О, да, приём Фейнмана (не он придумал, он популязировал его). Я подобное обычно по частям решаю, но тут он довольно хорошо залетает.
1 лайк
Ого, не знала о таком.Большое спасибо!!! Я интегрировала по частям, так можно было?
1 лайк
По сути да
\int u dv=uv-\int vdu \rightarrow \int\limits_{0}^{\infin} v^4 e^{\frac{-mv^2}{2kT}}dv=\int\limits_{0}^{\infin} v^3\left( e^{\frac{-mv^2}{2kT}}vdv\right)=-v^3 e^{\frac{-mv^2}{2kT}}\left(\frac{kT}{m}\right)\bigg|_0^\infin-\int\limits_{0}^{\infin}v^2 e^{\frac{-mv^2}{2kT}}dv
И так далее
4 лайка
Только сейчас вспомнил, что этот интеграл берется довольно красиво через полярные координаты и щепотки двойных интегралов. Для этого обозначим
I = \int_{-\infin}^{+\infin} e^{-\alpha x^2}dx
Если взять квадрат с обеих сторон, то мы получим следующее:
I^2 = \int_{-\infin}^{+\infin} e^{-\alpha x^2}dx \int_{-\infin}^{+\infin} e^{-\alpha x^2}dx
Поскольку здесь x является лишь “dummy variable”, можем заменить один из x на y, при этом принципиально ничего у нас не поменяется:
I^2 = \int_{-\infin}^{+\infin} e^{-\alpha x^2}dx \int_{-\infin}^{+\infin} e^{-\alpha y^2}dy = \int_{-\infin}^{+\infin} \int_{-\infin}^{+\infin}e^{-\alpha (x^2+y^2)} dydx
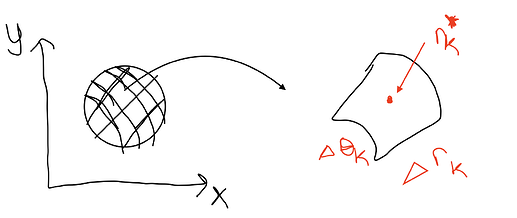
Вот здесь можно перейти в полярные координаты. Если сделать замену x = r\cos\theta, y = r\sin \theta, то можно сказать, что x^2 + y^2 = r^2. Далее, если в плоскости xy мы разбиваем регион интегрирования на бесконечно малые прямоугольники со сторонами dy и dx, то в случае замены, мы разбиваем этот регион (в качестве примера возьмем окружность) на вот такие круглые дольки (даже не знаю как их назвать):
Поскольку площадь сектора круга равна \pi r^2 \cdot \dfrac{\theta}{2\pi} = \dfrac{1}{2}\theta r^2, можно сказать что площадь конкретно рассматриваемой k-ной доли будет равна
\Delta A_k = \frac{1}{2}\Delta \theta_k \left(r_k^* + \frac{\Delta r_k}{2}\right)^2 - \frac{1}{2}\Delta \theta_k \left( r_k^* - \frac{\Delta r_k}{2}\right)^2 = r_k^* \Delta r_k \Delta \theta_k
Если сделать переход к пределу, то получится что dxdy = rdrd\theta. Таким образом,
I^2 = \int_0^{2\pi}\int_0^{+\infin} re^{-\alpha r^2}drd\theta
(раз уж интегрируем по всей плоскости xy, логично взять пределы интегрирования по r и \theta так, чтобы также интегрировать по всей плоскости).
А уже этот интеграл можно будет посчитать через обычную замену, и в результате получится, что I^2 = \dfrac{\pi}{\alpha}. А поскольку e^{-\alpha x^2} > 0 для любого x в \R, можно сказать, что
I = \int_{-\infin}^{+\infin} e^{-\alpha x^2}dx = \sqrt{\frac{\pi}{\alpha}}
18 лайков
По-моему, лучший способ определения моментов функции распределения Максвелла по скоростям, это сведение интеграла к Гамма-функции.
4 лайка