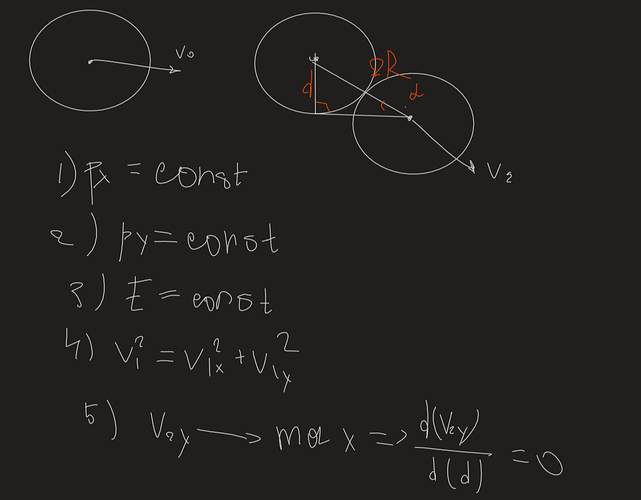В пункте 6 параграфа 28 в книжке Сивухина про это довольно полно написано
Ок спасибо
- Закон сохр. имп. на х
- Закон сохр. имп. на у
- Закон сохр. энерг.
- Выведи зависимость v2y от d
- Найди производную v2y по d и приравняй к нулю
- Реши получившееся уравнение и найди d
Через d и радиусы можно найти углы. Также используется тот факт, что скорость второго шара будет направлена по линии соединяющей центра шаров, так как именно по этой линии действует ударная сила реакции. Направление скорости первого шара после столконвения неизвестна, поэтому нужно просто написать v1x, v1y
А что делать если не знаю как использовать производную
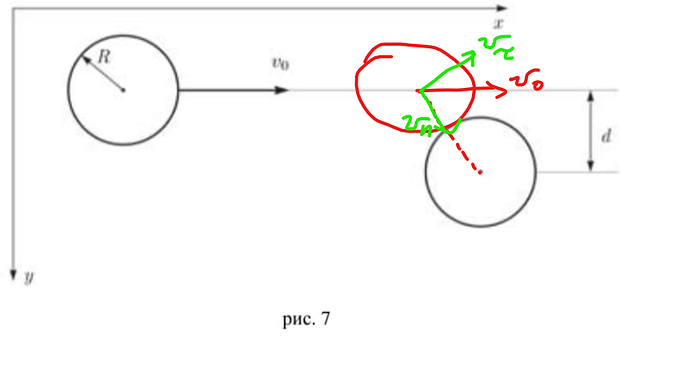
Как мне кажется, лучше разделять импульс на нормальный (вдоль оси которая проходит через центры) и тангенциальный (перпендикулярный нормальному). Тогда не будет проблем с тем, чтобы понять как всё сохраняется. Шайбы гладкие — трения между ними нет и тогда тангенциальный импульс сохраняется, а по нормальной оси просто записываем уравнения для абсоолютно упругого столкновения. Тогда если нарисовать, будет выглядеть как-то так
v_\tau никак не участвует в столкновении (так как она тангенциальная), поэтому её не трогаем. v_n полностью передаётся второму шарику. Поэтому приходим к выводу, что проекция скорости второй шайбы на ось Oy максимальна тогда, когда d = 2R (ну или если совсем строго, d = 2R - \delta, где \delta — какое-то расстояние очень близкое к нулю)
Последняя часть рассуждений немного быстрая, потому что её можно провести решая задачи 4.36 и 4.37 в 1001 задаче по физике