Напряженность полусферы

Физика Электромагнетизм
1

Задача 3. Найдите напряженность поля в центре равномерно заряженной полусферыю. Поверхностная плотность заряда равно \sigma .

Помогите решить задачу. Я раздели на тонкие крулгые пластины и 3 раз проинтегрировал ответ не вышел. как оптимально можно разделить эту полусферу

2 лайка
2

напряженность поля каждого кусочка сферы в центре действует по радиусу

d\vec{E} = k\frac{\sigma d\vec{S}}{R^2}

где d\vec{S} = S\vec{n}, тогда

E = k\frac{\sigma}{R^2}|\iint d\vec{S}| = k\frac{\sigma}{R^2}\pi R^2 = \pi k\sigma
E = \frac{\sigma}{4\epsilon_0}
6 лайков
3

Можете поподробнее разъяснить ваше решение

1 лайк
4

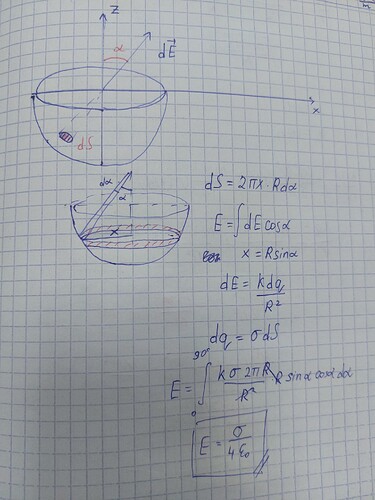
20240202_093031
20240202_0930311920×2560 301 KB

Вот решение если поделить на колечки толщиной Rd\alpha

4 лайка
5

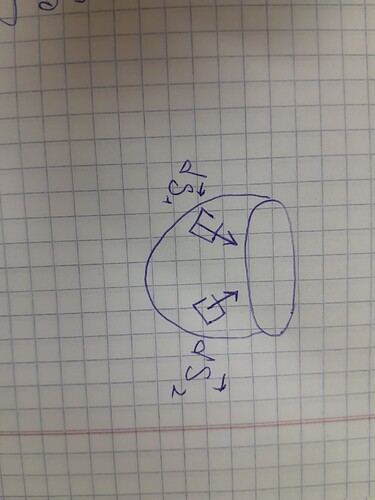
Если интересует подсчет того интеграла, то можно вот так геометрически увидеть, что они все складываются в окружность, как бы тень от полусферы получается

20240202_084944
20240202_0849441920×2560 161 KB

Так еще и результируюший вектор S направлен по направлению напряженности, из симметрии

3 лайка
6

Там разве из интеграла sinacosa не выходит [-1/4*cos2a] и там в знаменателе лишняя двойка?

7

да такой выходит интеграл, но ты же пределы не поставил

1 лайк