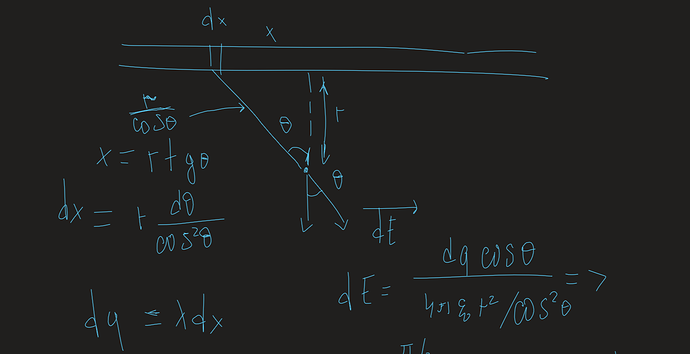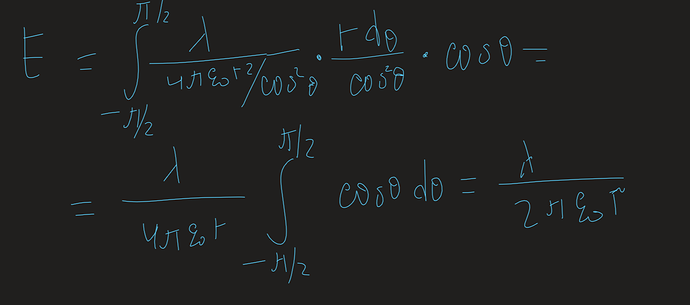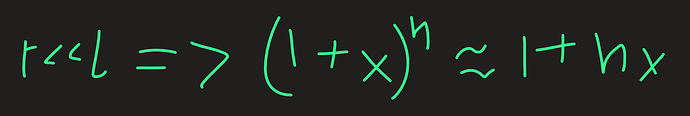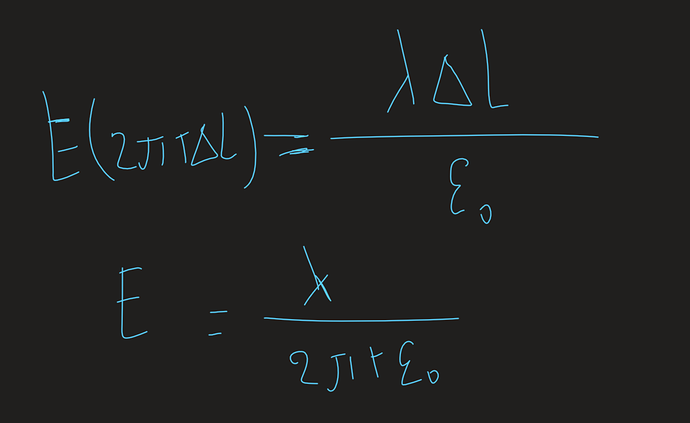1 лайк
Откуда задачи?
2 лайка
С задачника Иродов
Сначала рассмотрим малый элемент нити бесконечной длины:
Так как длина бесконечная, то пределы интеграла от -90 до 90 градусов (что в принципе логично)
Это выражение для напряженности нити бесконечной от длины как функция расстояния от нее понадобиться в дальнейшем.
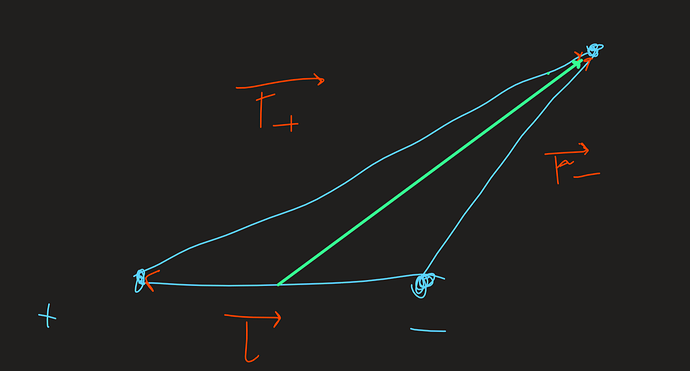
Теперь рассмотрим сам диполь:
Воспользуемся принципом суперпозиции для напряженностей, которая гласит, что вектор суммарной напряженности поля складывается из векторов напряженности отдельных элементов системы:
Дальше найди напряженности положительно и отрицательно заряженной нити относительно какой-то точки в плоскости. Учитывая малость l<<r ты можешь воспользоваться приближением:
(при дальнейших расчетах)
5 лайков
зачем так долго искать поле, если есть теорема гаусса)
ага. а потом в векторном виде домножаешь это на \vec r/r (с учётом знака заряда) и дальше так, как ты описал
1 лайк