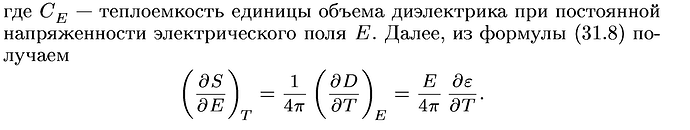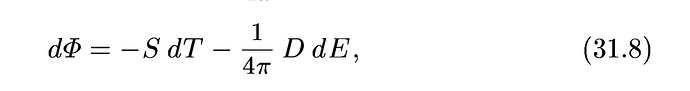1 лайк
Из формулы (31.8) если взять частную производную по температуре при постоянстве электрического поля, то получим
S = -\left(\frac{\partial\mathit\Phi}{\partial T}\right)_E.
Теперь возьмём ещё раз эту формулу (31.8) и возьмём частную производную, обратно, по электрическому полю при постоянстве температуры:
\left(\frac{\partial\mathit\Phi}{\partial E}\right)_T = -\frac{D}{4\pi}.
Снова из последнего получившегося уравнения возьмём производную таким образом:
\left(\frac{\partial}{\partial T}\left(\frac{\partial\mathit\Phi}{\partial E}\right)_T\right)_E = -\frac{1}{4\pi}\left(\frac{\partial D}{\partial T}\right)_E
По теореме о независимости смешанной производной от порядка дифференцирования (что, между прочим, также применялось в Сивухине, Том 2, параграф 45, пункт 2) имеем, что
\left(\frac{\partial}{\partial T}\left(\frac{\partial\mathit\Phi}{\partial E}\right)_T\right)_E =\left(\frac{\partial}{\partial E}\left(\frac{\partial\mathit\Phi}{\partial T}\right)_E\right)_T = -\left(\frac{\partial S}{\partial E}\right)_T.
Отсюда и получается всё.
7 лайков