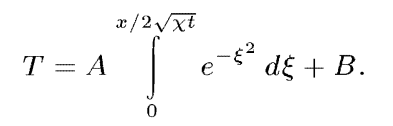
Читал я в Сивухине параграф про задачу об остывании полуплоскости и чёт не понял откуда он тут взял пределы и почему добавил константу?
я не знаю как нормально закинуть параграф, так что закину скринами
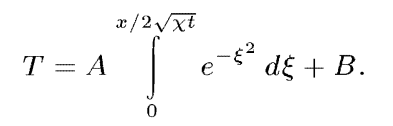
Читал я в Сивухине параграф про задачу об остывании полуплоскости и чёт не понял откуда он тут взял пределы и почему добавил константу?
Там видимо опечатка, и должно быть
А теперь вернемся к самому интегралу.
Если f'(t) является производной функции f(t), то имеет место следующее равенство:
Подставляя a = 0 и b = \xi,
А теперь заменяем f(\xi) = T.
Здесь f(0) имеет определенное значение и поэтому его просто можно заменить постоянной B.
Вообще мутный у него параграф получается, если опечатка в самом начале. Тогда возникает вопрос почему 2 в знаменателе берём здесь \xi=x/2\sqrt{\chi t}?
Остальное кажется понял, спасибо
Так удобнее и у нас не будет коэффициента в экспоненте для f'. То есть будет Ae^{-\xi^2}, а не Ae^{-\xi^2/4}.
спасибо