можете пожалуйста обьяснить, почему стабильность обителей, который заполнены полностью или наполовину намного выше остальных конфигураций? Я поняла общую тенденцию, что электроны более равномерно распределены, но хотелось бы услышать более подробные объяснения. ( В учебнике было обозначено 2 причины этого явления–spin-orbital coupling and electron exchange), но я не особо уловила суть(((
Спасибо за вопрос!!
Дамы и господа, запасайтесь попкорном, сейчас будет пафос.
Введение
Казалось бы, можно подумать – вопрос о школьной химии, не так ли? Почему мы говорим, что у азота “особо стабильная” конфигурация? Если мы останемся в рамках «школьной» химии – неизбежно придётся сказать «ну вот так вот)))»
Я так предполагаю учебник говорил что-то наподобие: присутствие электронов с одинаковым спином – стабилизирует систему (правило Гунда). А если к стабильной системе (скажем p3) добавляем еще электроны – мы ее дестабилизируем за счет Кулоновского отталкивания электронных пар.
And here we go! Что же магического в электронах с одинаковым спином? Ответ в квантовой химии.
Инструменты квантовой химии
Что есть волновая функция?
Допустим у нас есть два электрона: 1 и 2. В квантовой механике поведение электронов описывается некой волновой функцией \Psi. Сама по себе волновая функция не имеет физического смысла, но вот ее квадрат |\Psi|^2 – это плотность вероятности нахождения электрона. Что такое плотность вероятности? Ну смотрите, обычная плотность - показывает распределение массы. Помножив плотность на объем мы получаем массу. Точно также, помножив плотность вероятности на объем - мы получим вероятность нахождения электрона в этом регионе.
Скажем \chi_1 (\vec{x}_1) может описывать электрон 1. А \chi_2 (\vec{x}_2) описывает электрон 2.
Теперь, какую форму может иметь волновая функция, описывающая одновременно электрон 1 и электрон 2? Мы можем сделать допущение, что электрон 1 и электрон 2 не зависят друг от друга (подумайте, в каких случаях это допущение верно? в каких не верно?). Иными словами, вероятность найти электрон 1 в области x, а электрон 2 в области y – это просто произведение вероятности 1 в области x и вероятности найти электрон 2 в области y.
Тоже самое математически: |\Psi(\vec{x}_1, \vec{x}_2)|^2=|\chi_1(\vec{x}_1)|^2 |\chi_2 (\vec{x}_2)|^2
Интуитивно, что тогда \Psi(\vec{x}_1, \vec{x}_2)=\chi_1(\vec{x}_1) \chi_2 (\vec{x}_2).
Принцип Паули наносит ответный удар
Но тут есть одна проблема. И зовут эту проблему - Принцип Паули. На самом деле, формулировка принципа «два электрона не могут занимать одну и ту же орбиталь» - лишь упрощение более глобального принципа:
Волновая функция фермионов должна быть антисимметричной по отношению к перестановке любых двух частиц.
Примечание №1: теперь вы можете удивлять своих друзей и подруг
Примечание №2: а для бозонов - симметричной
Кто такие фермионы? Это частицы с нецелым спином. Например, мы знаем, что у электрона спин s=1/2. Электрон – фермион. Бозоны – частицы с целым спином. Например, у фотона спин s=1. Фотон – бозон.
Что такое антисимметричность? Это требование:
\Psi(\vec{x}_1, \vec{x}_2)= - \Psi(\vec{x}_2, \vec{x}_1)
Очевидно, что текущая форма \Psi не удовлетворяет этому требованию. Какая форма удовлетворит?
\Psi(\vec{x}_1, \vec{x}_2) = \chi_1(\vec{x}_1) \chi_2 (\vec{x}_2) - \chi_1(\vec{x}_2) \chi_2 (\vec{x}_1)
Поменяйте местами \vec{x}_1 и \vec{x}_2 и вы заметите, что получите то же выражение с обратным знаком. Это и есть антисимметричность.
Строгости ради надо помножить все добро на 1/\sqrt{2} ибо волновые функции должны нормализоваться на 1 (вероятность найти электрон в любой точки пространства – 1).
\Psi(\vec{x}_1, \vec{x}_2) = \frac{1}{\sqrt{2}} \left[ \chi_1(\vec{x}_1) \chi_2 (\vec{x}_2) - \chi_1(\vec{x}_2) \chi_2 (\vec{x}_1) \right]
Спин – не просто цифра
Фух, лучше. Теперь, давайте немного уточним из чего состоит \chi_i. Нам нужно описать где находится электрон в пространстве да? Пусть \psi_i(\vec{r}_i) - функция, описывающие положение электрона в пространстве. Вектор \vec{r}_i = \langle x_i, y_i, z_i \rangle описывает координаты в трехмерном пространстве. И че, \chi_i (\vec{r}_i) =\psi_i(\vec{r}_i) ?
Не совсем, нам нужно еще уточнить спин. Пусть \alpha (w_i) и \beta (w_i) это две функции описывающие спиновое состояние электрона i. \alpha – это электрон смотрящий вверх (m_s = 1/2), а \beta – смотрящий вниз (m_s= -1/2). Что такое w_i? Это координата, такая же как x_i, y_i, z_i в декартовом пространстве, только в спиновом. (и тут читатель задается вопросом: а че, спин это не просто циферка, там еще какое-то пространство есть? you live, you learn).
Важная заметка: \alpha и \beta это такие функции, что:
\int_{- \infty}^{\infty} \alpha^*(w) \alpha(w) dw =1
\int_{- \infty}^{\infty} \beta^*(w) \beta(w) dw =1
\int_{- \infty}^{\infty} \alpha^*(w) \beta(w) dw = \int_{- \infty}^{\infty} \beta^*(w) \alpha(w) dw =0
Простыми словами – каждая спиновая функция нормализуется на единицу и спиновые функции ортогональны друг другу. звездочка означает комплексное сопряжение. Кстати, если вы не знакомы с комплексными числами: на самом деле, квадрат любого числа – это произведение числа на его комплексно сопряженное. Например |\chi_i|^2 = \chi_i^* \chi_i. Мы об этом не задумываемся ибо у каждого действительного числа (то, с чем мы привыкли работать) комплексно сопряженное равно ему самому.
Замечательно. Теперь у нас есть все инструменты для ответа на вопрос.
АХТУНГ: форум обалдевает от такого длинного ответа, поэтому я разделю его на две части.
17 лайков
Частицы с разным спином.
Используя инструменты выше, запишем:
\chi_1(\vec{x_1}) = \psi_1( \vec{r_1}) \alpha (w_1)
\chi_2(\vec{x_2}) = \psi_2 (\vec{r_2}) \beta (w_2)
Напомню, что эти штучки мы суем сюда:
\Psi(\vec{x}_1, \vec{x}_2) = \frac{1}{\sqrt{2}} \left[ \chi_1(\vec{x}_1) \chi_2 (\vec{x}_2) - \chi_1(\vec{x}_2) \chi_2 (\vec{x}_1) \right]
Давайте посчитаем плотность вероятности:
|\Psi|^2 = \Psi^* \Psi = \frac{1}{2} \left[ \chi_1(\vec{x}_1) \chi_2 (\vec{x}_2) - \chi_1(\vec{x}_2) \chi_2 (\vec{x}_1) \right]^2
Ну что, раскроем скобки:
|\Psi|^2 = \chi_1^*(\vec{x}_1) \chi_2^* (\vec{x}_2) \chi_1(\vec{x}_1) \chi_2 (\vec{x}_2) -\chi_1^*(\vec{x}_1) \chi_2^* (\vec{x}_2)\chi_1(\vec{x}_2) \chi_2 (\vec{x}_1) + \chi_1^*(\vec{x}_2) \chi_2^* (\vec{x}_1) \chi_1(\vec{x}_2) \chi_2 (\vec{x}_1)- \chi_1^*(\vec{x}_2) \chi_2^* (\vec{x}_1) \chi_1(\vec{x}_1) \chi_2 (\vec{x}_2)
Вообще нас интересует (ну, читателя, возможно, пока это не интересует, но теперь будет) плотность вероятности как функция пространства. Нам если честно до лампочки где находится электрон в спиновом пространстве, нам важно знать где он в пространстве. Это можно легко устроить. Во-первых, давайте поймем, что вероятность нахождения электрона 1 в определенном пространстве \vec{x_1}, а 2 в \vec{x_2} это:
|\Psi|^2 d\vec{x_1} d\vec{x_2}
Напомню, что вектор \vec{x_i} коллективно определяет и пространственное, и спиновое положение электрона. произведение дифференциалов d\vec{x_1} d\vec{x_2} как бы определяет тот самый объем, на который мы умножаем плотность вероятности.
Т.е. если мы хотим работать с вероятностями, мы умножаем наше большое выражение (после раскрытия скобок) на d\vec{x_1} d\vec{x_2}. Давайте для простоты возьмем только первое слагаемое
\chi_1^*(\vec{x}_1) \chi_2^* (\vec{x}_2) \chi_1(\vec{x}_1) \chi_2 (\vec{x}_2) d\vec{x_1} d\vec{x_2}
Если мы распишем \chi_i на составные части, мы можем заменить d\vec{x_i} на d \vec{r_i} d w_i
\psi_1^*(\vec{r}_1) \psi_2^* (\vec{r}_2) \psi_1(\vec{r}_1) \psi_2 (\vec{r}_2) d\vec{r_1} d\vec{r_2} \cdot \alpha^*(w_1) \beta^* (w_2) \alpha(w_1) \beta (w_2) dw_1 dw_2
Я визуально разделил пространственные и спиновые функции т.к. они не зависят друг от друга. Сейчас мы имеем вероятность нахождения электрона i в пространстве r_i и со спиновый координатой w_i. Если нас интересует вероятность нахождения электрона i в пространстве r_i вне зависимости от спиновой координаты w_i – нам нужно просто сложить верхнее выражение для всех возможных значений w_i. Когда мы работаем с непрерывными величинами, сложение – это интегрирование.
Примечательный факт
Символ интеграла – это вытянутая S, от слова Sum
Т.е., мы интегрируем по dw_1 и dw_2, которые принимают значения от -\infty до \infty. Поскольку мы принимаем электроны независимыми друг от друга, мы можем интегрировать по каждой переменной по отдельности:
\int_{-\infty}^{\infty} \alpha^*(w_1) \alpha(w_1) dw_1 \cdot \int_{-\infty}^{\infty} \beta^* (w_2)\beta (w_2) dw_2
По определениям этих спиновых функций, оба множителя равны единице, и их произведение тоже равно единице. Повторяя эти действия со всеми слагаемыми, мы обнаружим, что второе слагаемое исчезает (ибо интеграл \alpha^*(w_1) \beta(w_1) равен нулю), та же участь ждет и четвертое слагаемое. А еще, пространственные функции можно записать чуть проще:
\psi_1^*(\vec{r}_1) \psi_2^* (\vec{r}_2) \psi_1(\vec{r}_1) \psi_2 (\vec{r}_2) = |\psi_1 (\vec{r_1})|^2|\psi_2 (\vec{r_2})|^2
По итогу:
|\Psi(\vec{r_1}, \vec{r_2})|^2 = \frac{1}{2} \left[ |\psi_1 (\vec{r_1})|^2|\psi_2 (\vec{r_2})|^2 + |\psi_1 (\vec{r_2})|^2|\psi_2 (\vec{r_1})|^2 \right] d\vec{r_1} d \vec{r_2}
Мы можем интерпретировать это выражение как: вероятность найти электрон 1 в точке \vec{r_1} и электрон 2 в точке \vec{r_2} это: вероятность найти их там если электрон 1 занимает волновую функцию \psi_1, а электрон 2 занимает волновую функцию \psi_2 ПЛЮС вероятность того же самого, только если электрон 1 занимает волновую функцию \psi_2, а 2 – \psi_1. По сути говоря, это результат того что нам не важно в какой функции находится электрон, главное что он там. Еще, поскольку вероятность найти два электрона - это просто произведение отдельных вероятностей, мы говорим что два электрона не коррелируют друг с другом.
Заметим важную (позже поймете почему) деталь:
|\Psi(\vec{r_1}, \vec{r_1})|^2 \neq 0
Частицы с одинаковом спином
Если, напротив, мы возьмем электроны с одинаковыми спинами:
\chi_1(\vec{x_1}) = \psi_1( \vec{r_1}) \alpha (w_1)
\chi_2(\vec{x_2}) = \psi_2 (\vec{r_2}) \alpha (w_2)
То, после таких же махинаций, мы получим:
|\Psi(\vec{r_1}, \vec{r_2})|^2 = \frac{1}{2} \left\{ \left[ |\psi_1 (\vec{r_1})|^2|\psi_2 (\vec{r_2})|^2 + |\psi_1 (\vec{r_2})|^2|\psi_2 (\vec{r_1})|^2 \right] - \left[ \psi_1^*(\vec{r_1})\psi_2(\vec{r_1})\psi_2^*(\vec{r_2})\psi_1(\vec{r_2}) + \psi_1(\vec{r_1})\psi_2^*(\vec{r_1})\psi_2(\vec{r_2})\psi_1^*(\vec{r_2}) \right] \right\} d\vec{r_1} d \vec{r_2}
Где мы имеем дополнительное слагаемое, которое содержит перекрестные множители. Иными словами, теперь уже, вероятность найти электрон 1 и 2 в определенной точке это не просто произведение отдельных вероятностей найти 1 и вероятности найти 2. Мы говорим, что движение электронов коррелирует.
Заметим, что в данном случае:
|\Psi(\vec{r_1}, \vec{r_1})|^2 = 0
Иными словами, вероятность найти два электрона с одинаковым спином в одной и той же точке пространства равна нулю. Кажется звучит знакомо, не так ли?)))
Вот вам еще способ выделиться среди одноклассников: исходя из этого, мы говорим, что вокруг электрона существует Fermi hole (там не может быть электронов с таким же спином).
Переходим к энергиям
Теперь, давайте подумаем, что значит то, что два электрона с разными спинами могут существовать в одной точке, а с одинаковыми нет.
Что будет если посадить два электрона в одну и ту же точку? Кулоновское отталкивание. Т.е. это нестабильно. И если мы имеем систему, в которой вероятность найти два электрона в одной и той же точке равна нулю – эта система будет стабильнее (ниже по энергии), чем система в которой эта вероятность не равна нулю.
На самом деле, вот этот феномен корреляции электронов – это фундаментальный концепт во всей квантовой химии. При рассмотрении, скажем, молекул (к примеру, простейшей \ce{H2}), окажется, что молекула становится стабильнее, чем два отдельных атома только благодаря присутствию т.н. exchange integral.
Если вернутся к уравнению:
|\Psi(\vec{r_1}, \vec{r_2})|^2 = \frac{1}{2} \left\{ \left[ |\psi_1 (\vec{r_1})|^2|\psi_2 (\vec{r_2})|^2 + |\psi_1 (\vec{r_2})|^2|\psi_2 (\vec{r_1})|^2 \right] - \left[ \psi_1^*(\vec{r_1})\psi_2(\vec{r_1})\psi_2^*(\vec{r_2})\psi_1(\vec{r_2}) + \psi_1(\vec{r_1})\psi_2^*(\vec{r_1})\psi_2(\vec{r_2})\psi_1^*(\vec{r_2}) \right] \right\} d\vec{r_1} d \vec{r_2}
Очень грубо говоря, первые два слагаемых могут стать т.н. coulomb integrals и обозначать кулоновское отталкивание двух электронов, а последние два – станут exchange integrals, которые будут понижать энергию системы.
В какой-то степени, можно сказать, что природа химической связи – в этом самом exchange integral.
Вот так вот можно ответить на изначальный вопрос о природе exchange effect
13 лайков
Some cool stuff
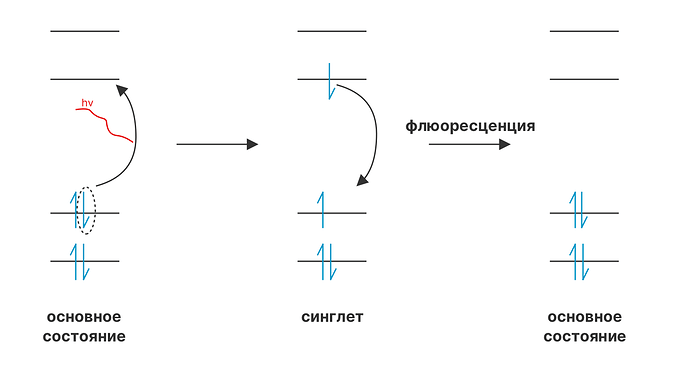
На самом деле, этот самый exchange integral встречается очень часто. Кто-то из вас может быть знаком с явлениями флюоресценции и фосфоресценции.
Если очень просто:
Флюоресценция – мы светим на что-то, и это что-то очень красиво горит. Мы убираем источник света и это что-то перестает красиво гореть. Не нравится.
Фосфоресценция – мы светим на что-то, оно начинает красиво гореть, а когда убираем источник света, оно продолжает некоторое время красиво гореть. Нравиться
В чем дело? Когда мы излучаем молекулу, мы переносим электрон с нижней орбитали на верхнюю. Но есть важный нюанс (приготовьтесь, щас у вас снесет башку) – важно учитывать спин.
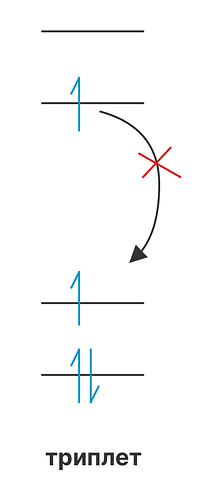
Если каким-то чудом мы сможем получить триплетное состояние:
Переход с триплетного состояния в основное называется фосфоресценцией. Но обратный переход уже не так прост, ибо электрону нужно сначала поменять спин. Поэтому этот процесс медленный (и длится дольше флюоресценции).
А еще триплетное состояние ниже по энергии, чем синглетное (почему? потому что exchange integral), а значит если для возбуждения нам нужно было УФ излучение (с короткой длиной волны, большой энергией), то при релаксации энергия выделяющейся электромагнитной волны меньше, длина волны больше и сама волна переходит в область видимого света. Т.е. свечение становится обычным, не ультрафиолетовым!
Ребята, если вы еще не визжите от восторга – самое время.
Выводы, мораль
- Химия – это офигенно.
- Смотри пункт 1.
- Химия не ограничивается тем, что мы видим в школе. В школе мы даже весь айсберг не успеваем покрыть.
- Для хорошего понимания основ химии – нужна серьезная математическая и физическая база.
Теперь впервые поделюсь очень важной для меня мыслью: хороший учитель обладает знаниями за гранью того, что он преподает детям. Порой дети могут задать вопрос, формулировка которого простейшая – но ответ требует глубочайшего понимания предмета. И если на вопрос ребенка ответить «ну вот так вот, прими» – вряд ли это поспособствует его интересу. Теперь, я не берусь утверждать, что большинство читателей поняли что только что произошло – но самое главное не это. Самое главное – я обозначил вам горизонт. Я показал что ответ есть – просто до него нужно дорасти. Я показал, что химия может быть очень точной. Я показал что фундаментальная наука объясняет какие-то крутые явления.
На самом деле, если вас заинтересовал пример с возбуждением молекул – этим занимается физическая органическая химия. Процессы возбуждения и спиновые состояния играют ключевую роль в любых дисплеях. Экран вашего ноутбука – продукт фундаментальных исследований физорганики. Два основателя Intel – это PhD по физике с MIT и PhD по химии с калтеха.
И вам не обязательно понимать всю квантовую химию, чтобы согреваться от мысли что то, чем вы пользуетесь основывается на квантах.
18 лайков
Если я правильно понимаю, то это будет тем ближе к реальности, чем дальше будут находиться два электрона, то есть чем меньше перекрывание их орбиталей. То есть, при большем перекрывании орбиталей, увеличивается стабилизация конфигурации, но при этом уменьшается точность модели. Тогда у меня вопрос, в какую сторону наша модель ошибается при значительном перекрывании орбиталей? Мы недооцениваем стабилизацию или переоцениваем ее?
А тут весело получается. На самом деле, использование произведения отдельных волновых функций оправдывается не сколько вероятностными соображениями, сколько линейной алгеброй.
Мы знаем, что волновая функция должна быть собственной функцией гамильтониана. Если гамильтониан состоит исключительно из локальных операторов (не включает электрон-электронные взаимодействия, а лишь кинетическую и потенциальную энергию электронов) – то это простая сумма операторов, действующих по отдельности на каждую \psi, а сумма операторов и приводит к произведению в волновой функции.
Теперь мы можем задаться вопросом – а что если включить электрон-электронное отталкивание? Если считать его прямо – у нас будет немного другая форма гамильтониана, но, что примечательно – когда мы установили антисимметричность волновых функций, мы, в какой-то мере отошли от «независимости» (беру в кавычки поскольку нам не сильно нужно было допускать что-то о независимости, это было больше следствие формы операторов) электронов и уже антисимметричная волновая функция может быть собственной для полного гамильтониана.
3 лайка
Спасибо, а в каком учебнике/лекции можно будет прочитать про это?
вам именно про exchange effect или квантовую химию/физику в целом?)
1 лайк
в целом, лучше наверное учебник про кванты, если на доступном школьнику (с хорошими базовыми знаниями) уровне.
Хм… тяжелый вопрос. Я тяжело себе представляю как кванты читать без знания линейной алгебры. Но всё что без неё (т.е. для школьников) слишком просто и базово, там на веру такие эффекты берут. А всё что сложнее, уже требует линал.
Ну, я думаю McQuarrie Quantum Chemistry вполне по силам до определенных глав. И я бы начинал с него (если вы химик). Если же есть сильная база по математике и физике, можно попробовать осмелиться на Griffith Introduction to Quantum mechanics
А матан можно взять на OCW:
5 лайков
Еще лекции МГУшные доступны на ютубе. Там есть очень хорошие курсы по квантам или введению в кванты.
1 лайк
Кстати) @DrMrmld @Madsoul @SanzharB @Chemistred
нарисуйте диаграмму МО молекулы кислорода
1 лайк
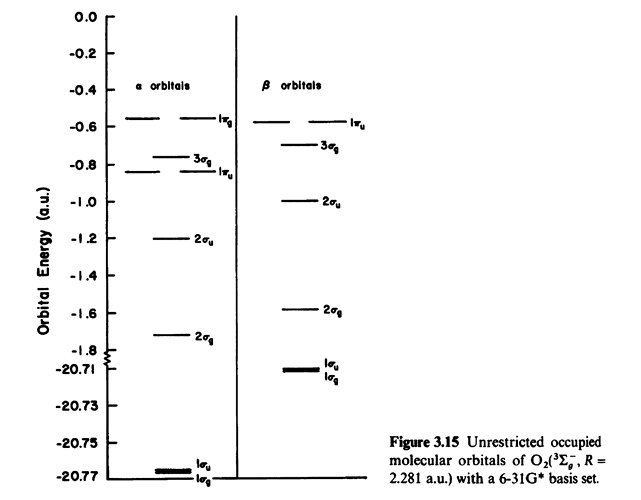
Отлично. Именно такую картинку мы получим если найдем волновые функции методом Хартри-Фока, считая, что у двух спаренных электронов \alpha и \beta пространственные части одинаковые (вполне разумное предположение)!.
А теперь посмотрим на \pi^* орбитали. На них \alpha электроны. Теперь посмотрим на все нижестоящие электроны: есть куча заполненных орбиталей, на которых \alpha и \beta электроны. С каждым из них у \alpha электронов \pi^* орбитали будет Кулоновское отталкивание. Но с каждым из \alpha электронов будет еще и exchange interaction (отрицательное по знаку/стабилизирующее). Т.е. электроны в \pi^* будут как бы стабилизировать все \alpha электроны ниже. И если мы позволим электронам \alpha и \beta спинов иметь разную пространственную функцию, мы получим такую картинку:
6 лайков