Пишут, что молекула может растягиваться и изгибаться только на определённых частотах, а это как вообще, то есть молекула будет как-то двигаться только в том случае, если на неё будет падать электромагнитное излучение определённой частоты?
Молекула поглощает энергию, если частота излучения соответствует частоте вибрации, иными словами молекула изначально имеет какое-то значение частоты которое оно может поглощать?
Результатом поглощения является увеличение амплитуды, или же два атома будут растягиваться и сжиматься немного дальше. А как поглощение некой частоты может повлиять на амплитуду, это как две одинаковые волны сталкиваются, и образуется другая волна с большей амплитудой?(а что даёт амплитуда?) И как амплитуда/поглощённая частота связаны с тем, как буду растягиваться два атома?
давайте с перва назовем это не поглощением частот а поглощением волн))
думаю да вы правы, в молекуле между связанными атомами происходит bond scretching под поглощением определенных частот волн. Ну из за этих movements группы в молекуле показываются в детекторе.
и кстати думаю вам надо бы посмотреть какой ни будь видос про IR spectroscopy чтобы поверхностно понять логику процесса а потом уже углубляться в книжке
Chemistry Jesus))
так я называю этого учителя) он реально Jesus по химии)) объясняет понятно и быстро и там так же говориться про bond scretching
http://chem.spbu.ru/files/Vladimir/Vasiliev/new-277_InfraRedSpektr.pdf
http://www.physchem.chimfak.sfedu.ru/Source/special/ir_spectr_1.html
Я посмотрел видео, вроде все понятно, но там не было ответа на вопрос про амплитуду, не знаете ответа?
ну при поглощение волн молекула делает молекулярные колебания которые и влияют
на амплитуду. Чем сильнее и больше эти движения молекул тем длиннее будет амплитуда думаю.
Под «Молекулярные колебания» имеете ввиду растяжение и сжатие связей да? А вот интересно как амплитуда и растяжение связей связаны
ну да движение молекул, с верху немного попутал. В общем наоборот поглощение каких то волн в конкретной частоте влияет на амплитуду движения соединенных атомов. Ты наверное спрашиваешь как будет влиять частота на амплитуду волн а не на амплитуду движений молекул но тут думаю говориться именно про движение молекул
Вот есть электронные уровни энергии. Мы говорим, что электрон либо на 1s либо на 2s. У него либо -13.6 eV либо, там, не знаю, -5 eV. И ничего посередине.
Точно так же есть колебательные уровни энергии. Они тоже квантизированы[1]. Эти уровни энергии определяются незамышленной формулой:
Каждому значению v соответствует определенное (одно) колебание. Это колебание характеризуется каким-то вектором, который определяет что это за колебание (растяжение, сгибание и т.д.) и определяет амплитуду. Амплитуда НЕ определяется частотой поглощенного света, амплитуда определяется самой природой колебательного уровня (а природа – результат решения уравнения Шредингера).
Молекула имеет структуру колебательных уровней по энергии. И поглощенная энергия используется только для перехода от одного уровня к другому.
Вот хорошая картинка:
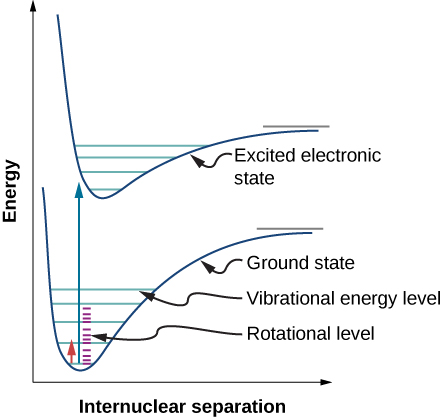
Большие параболоиды соответствуют одному электронному уровню (скажем основное состояние: атом водорода и электрон на 1s и возбужденное: атом водорода и электрон на 2s)
В каждом электронном состоянии есть куча колебательных уровней[2].
Чем больше амплитуда (еще раз напомню, определенная самой природой колебательного уровня) показывает насколько сильно атомы будут растягиваться или сгибаться.
У уровней с низким v амплитуда будет скорее всего меньше, чем у уровней с высоким v.
Есть разница между амплитудой волн и амплитудой движения молекул (что это)? Я что-то совсем запутался…
вот это:
можно смело выбросить из головы и еще раз прочитать то, что я написал.
))))))))))))) yeah
А что за v?
А что за колебательные уровни? В МакМюрри про это вроде не было
А что на той картинке параболоид?
Значит молекулы самого начала могут поглощать электромагнитные волны определённой частоты, и если у этих волн большая амплитуда, то молекулы когда поглотят эти волны(энергию от них), они будут сильнее растягивать связь, чем если бы они поглотили волны с меньшей амплитудой, так?
А когда молекула поглощяет волну, «определённая природой» амплитуда ведь увеличивается? А как это происходит, и вообще у молекулы до поглощения нету ведь никакой амплитуды, а как она может увеличиться если ее нету?
Это все относится ведь к квантам? А они и вправду трудные
Просто целое число v=0,1,2,\dots. Его можно назвать квантовым числом для колебаний. Такое же квантовое число как и n,l,m_l, m_s, которые у нас есть в атоме водорода.
Поскольку квантовые системы (в подавляющем большинстве) соответствуют “квантизированию” чего-то, рано или поздно появится переменная, которая и будет показывать эту квантизацию. То, что v=0,1,2,\dots а не, скажем, v\in \mathbb{R}, и есть следствие квантизации.
Не было, это учебник по органике, а колебательные уровни – это квантовая химия.
В рамках изучения органики возьмите их за данность, так же как вы берете за данность существование электронных орбиталей.
Правильней сказать “что-то похожее на параболу”
Забудьте про амплитуду электромагнитных волн. Энергия ЭМВ зависит только от частоты ЭМВ. Амплитуды в уравнении E=h\nu нет.
Так еще раз.
Очистили голову, забыли все. В голове пустой лист:
- Вас изначально интересовало почему молекулы могут поглощать только определенные частоты ЭМВ.
- Я вам говорю, в молекуле есть набор колебательных уровней с разной энергией. Эти уровни не непрерывны, а дискретны (квантизированы). Молекула может быть на уровне v=0,1,2,\dots. Молекула не может быть на уровне v=1.00001 или v=1.23456. Энергия уровня v определяется как E_v=k(v+1/2), где k константа пропорциональности.
- Делаем вывод: молекулы поглощают только волны с определенной частотой (энергией), потому что поглощенная энергия используется для перехода на другие колебательные уровни, которые обладают определенной энергией.
Все, на этом вопрос закрыт. В п. 2 и п. 3 есть ответ на вопрос из п. 1. Энергия ЭМВ зависит только от частоты ЭМВ (и никакие амплитуды здесь не появляются), а энергия колебательного уровня зависит только от v, от некого квантового числа. Повторюсь, вопрос закрыт.
Дальше вы можете задаться вопросом:
- Хорошо, я все понял. Но мне интересно, а что определяет константу пропорциональности k?
- Я вам говорю: каждое квантовое число v соответствует определенным колебаниям. Колебания – это любые смещения атомов относительно их равновесных позиций. И вот константу k мы получаем когда решаем уравнение Шредингера для таких смещений. Так получается, что k=h/2\pi \sqrt{k/m}. Поскольку при переходе с любого уровня v на уровень v+1 нам нужно поглотить энергию E=h/2\pi \sqrt{k/m}, а мы знаем что энергия имеет общий вид h\nu, мы можем сказать, что а давайте обзовем h/2\pi \sqrt{k/m}=\nu. И коль она имеет размерность частоты, назовем ее частотой. Поскольку речь идет про колебательную энергию, давайте назовем “vibrational frequency”. Заметим, что строго говоря “vibrational frequency” не всегда тоже самое, что “frequency of vibrations”.
Вопрос закрыт.
Дальше, вы можете задаться вопросом:
- Мы говорим о колебаниях, а мы знаем как эти колебания выглядят? Мы можем посмотреть?
- Да, знаем и можем. Там довольно страшные волновые функции, которые я показывать не буду.
И прежде чем вы захотите сказать: “тогда все обман и без ответа на вопрос из п.6. все предыдущие ответы обнуляются” я вам приведу аналогию с электронными орбиталями.
Вы же знаете, что энергия ионизации водорода 13.6 eV (а значит энергия 1s орбитали -13.6)? Вы можете, знать что энергия 2s -3.4 eV. Вы можете сказать, что для возбуждения электрона надо поглотить 13.6-3.4=10.2 eV энергии. Вы можете посчитать частоту ЭМВ, соответствующую этой энергии.
Но вы ничего не знаете про амплитуду ЭМВ и, самое главное, для ответа на вопрос вам это не нужно.
Для ответа на вопрос «сколько энергии надо на возбуждение», вам не нужно знать форму орбиталей 1s или 2s. Когда вы говорите про поглощение ЭМВ для возбуждения, вы не говорите о том как меняется форма орбитали, во что она превращается, как именно она меняется. Конечно, если вы хотите, вы можете это посмотреть – но это будет уже другой вопрос.
Дальше, я вам говорю, что энергия колебательных уровней зависит от квантового числа v. Этой информации достаточно, так же, как и достаточно обозначений 1s и 2s (что тоже, не больше, чем квантовые числа n=1, l=0 и n=2, l=0) для понимания о какой энергии идет речь.
Вы же, в контексте электронных возбуждений не пытаетесь понять как меняется волновая функция? Вот точно так же и не надо примешивать вопрос “формы колебательных уровней” к “энергии колебательных уровней”.
Да
Если вы откроете МакМуррик на 10 главе и дадите ученику 11 класса (не олимпиаднику) на уроке школьной химии, он вам скажет тоже самое. Но вы ее понимаете с учетом того, что вырабатывалось в предыдущие 9 глав.
В квантах тоже самое[1]. Если вы пытаетесь сразу понять “природу” квантов запрыгнув на тему условной 10 главы, пропустя первые 10 глав, то, конечно, вы ничего не поймете.
И здесь ключевой навык – абстрагирование. Пока вы изучаете органику вам предлагается простая модель: есть набор уровней по энергии, каждый описывается формулой E=f(v). Этого достаточно для понимания всей информации, которая связан с колебаниями в органике.
Если вы захотите узнать откуда берется f(v), вы пойдете изучать кванты. Когда вы узнаете, вы, безусловно, будете знать больше об этом мире, будете более преисполнены прекрасным, приблизитесь к космической гармонии и будете совершенно другим человеком.
Но в контексте органики вам это не добавит ничего, это ничего не изменит, потому что самое главное (в органике) это чему равно E, а не откуда оно берется. Поэтому если вы хотите быть только органиком, вам достаточно знать форму f(v).
Применимо к любому знанию, на самом деле. ↩︎
Больше спасибо за ответ, не буду слишком углубляться в детали
