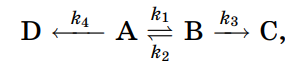То что надо использовать квазиравновесное приближение - правда. При равновесии скорость двух реакций равны, r_1=r_2. Cкорость расходования А я выражу через концентрацию В:
\frac{k_1}{k_2}=\ce{\frac{[B]}{[A]}}\tag{1}
-\frac{\ce{d[A]}}{\ce{dt}}=r_1-r_2+r_4=r_4=k_4\ce{[A]}\stackrel{(1)}{=}\frac{k_2k_4\ce{[B]}}{k_1}
-\ce{\frac{d[B]}{dt}}=r_2-r_1+r_3=r_3=k_3\ce{[B]}
Скорость расходования обоих равна
\ce{-\frac{d[A] + d[B]}{dt}}= \frac{k_2k_4\ce{[B]}}{k_1}+ k_3\ce{[B]}=\ce{[B]}\left( \frac{k_2k_4}{k_1}+k_3\right)\tag{2}
А теперь прочитаем условие.
Вначале в системе присутствует только мономер, начальная концентрация [A]0. При высоких температурах быстро устанавливается равновесие между мономером и эксимером, в результате чего распад обоих происходит с одной и той же эффективной константой скорости.
То есть у нас в начале только А. При высоких температурах быстро устанавливается равновесие. Это начало, А быстро перешел в В, и они еще не успели распаться на С и D. Теперь, когда они в равновесии, они будут распадаться с одинаковой эффективной константой. Я принимаю что [C]=0, [D]=0.
\begin{gathered}\ce{[A]_0 = [A] + [B]}\stackrel{(1)}{=} \frac{k_2\ce{[B]}}{k_1}+\ce{[B]}=\frac{\ce{[B]}(k_1+k_2)}{k_1}\implies
\\
\implies\ce{[B]}=\frac{k_1\ce{[A]_0}}{k_1+k_2}
\end{gathered}
Вставим это выражение для В, в уравнении 2
\begin{gathered}
\ce{-\frac{d[A] + d[B]}{dt}}= \frac{k_1\ce{[A]_0}}{k_1+k_2} \left( \frac{k_2k_4}{k_1}+k_3\right)=\frac{k_2k_4+k_1k_3}{k_1+k_2}\ce{[A]_0}=
\\
=k_{eff}\ce{[A]_0}\ ,\ \ \ \ \ \ \ \ \ \ \ где\ \ \ k_{eff}= \frac{k_2k_4+k_1k_3}{k_1+k_2}
\end{gathered}
Вот такое вот решение предложил @Meirzhan