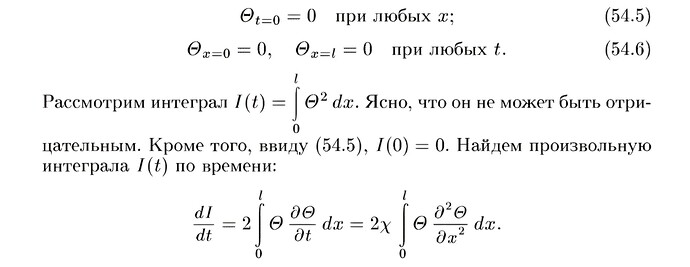Здравствуйте. Прошу тех, кто разбирается в этой теме, предложить простую статью или книгу для понимания вариационного исчисления, которое используется в книге Сивухина для теоремы единственности.
Серьезный запрос. Вариационное исчисление это где-то между мат.анализом и функциональным анализом. Если я не ошибаюсь, не так давно Вы задавали вопрос про частные производные. Чтобы скакнуть в понимании от частных производных до вариационного исчисления, нужно много времени и занятий математикой.
1 лайк
Хорошо, в этом случае явно более оптимальным будет найти другой способ доказательства данной теоремы.
в душе не чаю что такое вариационное исчисление но д-во вроде понятное(помимо момента когда он берёт I(t) = \int_0^l \Theta^2dx), с чем у тебя проблемы?
2 лайка
Аа я сам разобрался, там просто нужно
\frac{d}{dx} \left( \int_{a}^{b} f(x, t) \, dt \right) = \int_{a}^{b} \frac{\partial f(x, t)}{\partial x} \, dt.
Просто я показал это знакомому, и он сказал, что такие задачи в основном решаются в математике с помощью вариационного исчисления.
1 лайк