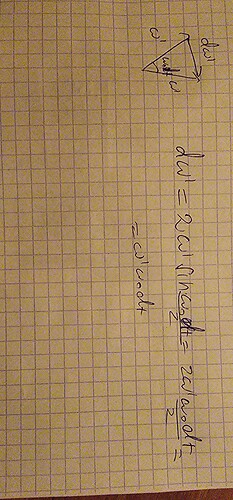Иродов, механика задача 1.10
Как вывели формулу для приращения модуля вектора угловой скорости, |dω’’|=ω’ω0dt
2 лайка
Теорема косинусов
Понятия не имею как в учебниках это выводят, но можно ещё вот так
\frac{d \vec \omega '}{dt}=\omega' \frac{d \vec i}{dt} + \vec i \frac{d\omega '}{dt}=
\omega' \frac{d \vec i}{dt}
\vec i = (\cos \alpha, \cos \beta); \alpha, \beta - углы между осями координат и вектором
\frac{d \vec i}{dt} = (-\sin \alpha \frac{d\alpha}{dt}, -\sin \beta \frac{d \beta}{dt})
|\frac{d\vec i}{dt}| = \sqrt{ \omega_0 ^2 \sin^2 \alpha + \omega_0 ^2 \sin^2 \beta} = \omega_0
|\frac{d \vec \omega'}{dt}|=\omega ' \omega_0
В более общем случае это вроде как выглядит так
\frac{d \vec \omega'}{dt}= \vec \omega_0 \times \vec \omega'
5 лайков