У меня два вывода, первый скорее корректировка строки в книге:
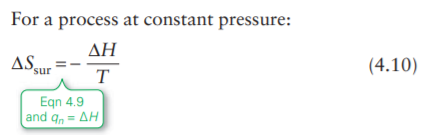
У окружающей среды(вселенной) давление никак не изменяется с ЛЮБЫМ изменением в системе, т.о. ведь q=DH, и получается что необязательно ведь p=const у системы, так зачем авторы подписали к этой формуле обязательным условием использования const=p для САМОГО процесса в системе?
Второе это необычное вычисление происходящее из того, что т.к. DH=q для окр.среды(вселенной), что q(rev) нам необязательно rev при расчётё DS sur, следовательно, при расчётё S total для процесса передачи энергии(путём тепла), мы, в системе S считаем как для rev process, а т.е. так:

При выводе этой формулы мы допускаем намеренно пренебрежимо-малую ошибку считая бесконечно малое изменение в температуре - постоянной температурой для всего процесса потому что нам важно это для обратимости процесса, необходимой для энтропии системы(q rev). Поэтому, для расчёта DS sur при heating, мы не делаем этой ошибки(и пишем dT в знаменателе), И СЛЕДОВАТЕЛЬНО СОКРАЩАЮТСЯ ТЕМПЕРАТУРЫ:

и получается что DS sur = C. Из этого исходит всего то, что S total =
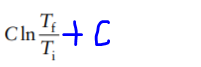
, где дописанная мною синим цветом +С обозначает теплоёмкость(полученная из сокращения температур на прошлом фото).
Пожалуйста, ответьте, верны ли мои два вывода? Я буду неимоверно благодарен вам! Так как считаю эти выводы воистину хорошим доказательством того, что изучаю главу нормально!
Начнем с того, что по фундаментальному определению dS = \frac{dq_{rev}}{T}. Формула применима как и для системы, так и для окружающей среды. Поскольку окружающая среда чрезмерно большая, по сравнению с системой, любые изменения происходящие в системе приводят к лишь пренебрежительным изменениям в окружающей среде. Допустим, в ходе какого-то процесса в системе, в окружающую среду выделилось 1 моль углекислого газа. В то же время в атмосфере находится изначально 100 000 моль углекислого газа (условно). И понятное дело, что между 100 000 и 100 001 разницы практически нет. Именно поэтому давление окружающей среды остается постоянным независимо от процесса. Точно также можно рассуждать про температуру и объем окружающей среды.
Возвращаясь к вопросу, предположим что система потеряла -q энергии в виде тепла. По закону сохранения энергии, эта энергия должна выделяться в окружающую среду. Получается, в ходе процесса окружающая среда поглотила +q энергии в виде теплоты. А вот тут и вступает в дело постоянство окружающей среды. Поскольку передача теплоты в окружающую среду сопровождается постоянным давлением, объемом и температурой (последний фактор отвечает за обратимость передачи, ибо тепловое равновесие), можно считать что теплота передается в окружающую среду обратимо, независимо от того, обратимый/необратимый процесс протекал в системе, ибо мы рассматриваем лишь окружающую среду в данном случае. Значит dS_{sur} = -\frac{dq_{sys}}{T} (заметим, что q_{sys}=-q_{sur}).
Что мы сделали ? Мы выразили изменение энтропии окружающей среды через происходящие изменения в системе, и теперь нам остается лишь рассматривать саму систему. Если процесс в системе сопровождается постоянным давлением, то уравнение (4.10) в книге будет справедливым. Если процесс в системе не сопровождается постоянным давлением, то увы, уравнение (4.10) в книге уже не будет применимым.
Твоя ошибка в рассуждениях скорее заключалась в том, что ты рассматривал изменения чисто с точки зрения окружающей среды, в то время как формула (4.10) наглядно показывает нам, что изменение энтропии окружающей среды связано с изменениями в системе.
На данном этапе думаю понятно что причина сие “вычисления” кроется в другом, а не в том что dH =dq
На самом деле, изменение энтропии в системе считается по формуле для обратимой передачи теплоты потому что энтропия - функция состояния не зависящая от пути достижения конкретного состояния. Это означает что если будет протекать один и тот же процесс с отличием в обратимости передачи , то изменения энтропии этих процессов будут одинаковыми, ибо функциям состояния абсолютно фиолетово на то, каким образом было достигнуто то или иное состояние. Им важен лишь результат.
Когда я читал, для наилучшего понимания приводил аналогию между функцией состояния и олимпиадником, который гонется за медалями. Такому олимпиаднику не важно каким способом он будет чалить, ему важен лишь конечный результат
Я бы сказал, что это скорее не ошибка, а просто “convenience”. В предыдущих главах было четкое обоснование по трем вопросам касательно фундаментальной формулы определения энтропии (dS = \frac{dq_{rev}}{T}) :
- Почему именно обратимая передача теплоты ?
- Почему именно теплота, а не работа ?
- Почему температура находится в знаменателе ?
В данном случае нам интересен ответ на первый вопрос. Если перечитать строчки, то в принципе должно быть понятно, что обратимые передачи легче всего измерять, поскольку необратимые передачи теплоты не совсем плавные и их довольно проблематично как-то да пытаться измерять.
Короче говоря, то что температуру в знаменателе взяли просто как постоянную температуру означает то, что таково условие для обратимой передачи энергии, а следовательно, обязательное условие для расчета изменения энтропии.
Это противоречит формуле (4.10) которую автор вывел и преподнес читателю. Весь прикол обратимости процесса заключается в том, что в конечном счете, для обратимых процессов суммарное изменение энтропии вселенной равно нулю. Покажем это расчетами.
Поскольку процесс в системе обратимый, можно считать что \Delta H = q_{sys} = \Delta S_{sys} \cdot T = CTln\frac{T_{f}}{Ti}. По формуле (4.10) изменение энтропии окружающей среды составляет \Delta S_{sur} = -\frac{CTln(\frac{Tf}{Ti})}{T} = -Cln(\frac{Tf}{Ti}). Так как изменение энтропии вселенной равно сумме изменений энтропии системы и окружающей среды, понятно что \Delta S_{universe} = 0.
Точно, спасибо!
Всё разложил по полочкам, спасибо.
Не понял, а зачем нам постоянство объема? Хватает же давления. Тогда мы скажем что эту теплоту можно заменить на изменение энтальпии, а изменение энтальпии функция состояния. Поэтому не важно проходили ли мы через бесконечно малые шаги или нет.
А еще, Эткинс ведь явно говорил что ЛИБО давление ЛИБО объем окружения берется постоянной. Вот пруф
The surroundings, which can be modelled as a large water bath, remain at constant temperature regardless of how much energy flows into or out of them. They are so huge that they also have either constant volume or constant pressure regardless of any changes that take place to the system.