A gas effuses into a vacuum through a small hole of
area A. The particles are then collimated by passing through a very small circular hole of radius a, in a screen a distance d from the first hole. Show that the rate at which particles emerge from the second hole is \frac{1} {4} nA<v>\frac{a^2}{d^2}, where n is the particle density and is the average speed. (Assume that no collisions take place after the gas effuses through
the second hole, and that d >> a.)
Я делаю так, число молекул прошедших через первое отверстие в единицу времени \Phi= \frac{1}{4}n \overline{v}A, я предполагаю что после прохождения через отверстие скорости останутся изотропным распределёнными и число молекул попавших во второе отверстие найдётся вот так \Phi \frac{\Omega}{2\pi}=\Phi \frac{2\pi \sqrt{d^2+a^2} (\sqrt{d^2+a^2}-d)}{2\pi(d^2+a^2)}=\Phi \frac{a^2}{2d^2} , делю на 2\pi так как назад лететь не могут. Получается выражение вдвое меньше ответа, я уже задавал подобный вопрос Савченко 5.1.10, но мне там ответили, что должно быть вдвое меньше. Мне кажется есть какая-то ошибка в рассуждениях. Помогите пожалуйста
У тебя не выходит, потому что там надо по обычным углам интегрировать (в телесных углах просто синус, но когда учитываешь скорости там выражение умножается на косинус). Если что, сивухин 75 параграф.
Интеграл от 0 до \frac{a}{d}
Либо я совсем дурак, либо это не решает проблему. У меня всё ещё выходит вдвое меньше.
Я делал так же как и при обычной эффузии, взял участок v \cos\theta до второй стенки, потом A'\frac{d \Omega}{2\pi} n v \cos \theta, (2\pi тк назад не двигаются) теперь интегрируем и получаем \Phi'=A'\frac{1}{2}n' v \frac{a^2}{d^2}, но n' это не начальная концентрация, а конкретно в той точке. \Phi постоянно, поэтому концентрацию можно выразить n=\frac{\Phi}{A' v} подставим, получим ответ вдвое меньше, чем должно быть
Вообще останутся ли скорости изотропными после эффузии?
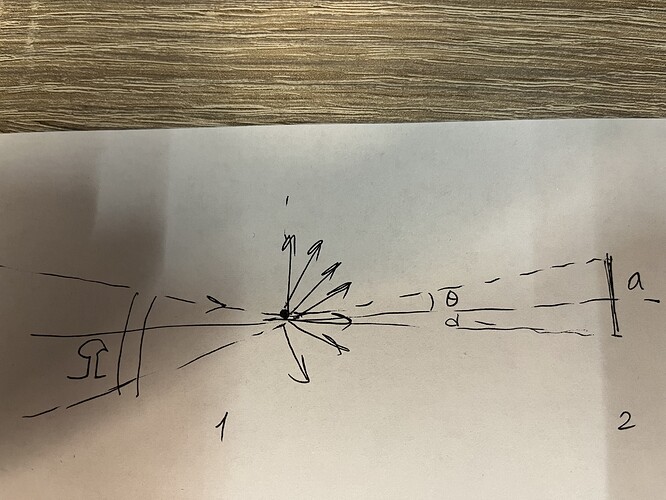
Смысл нашего интегрирования по углу в том, что мы как бы “отбираем” только те частицы в первой дыре, которые смогут попасть во вторую. Рисунок примерно следующий:
Ну а выходит там все нормально:
а что не так с моими рассуждениями?
постоянно, поэтому концентрацию можно выразить
Я тут не особо понял ход мыслей, можешь подробнее объяснить?
типа скорость не зависит от времени, поэтому в каждую единицу времени будет выпускаться одинаковое количество молекул, возьмём что у всех одинаковая скорость, тогда концентрация молекул которые движутся под одинаковым углом будет постоянна и типа за единицу времени будет n=\frac{\Phi}{A'v \cos\theta} кажись я нашёл ошибку
@PoMa Hello, I am not from Russia, so can you please tell me where I can find a pdf of sivukhin.
If you need the English version, then I can not help you, sorry. But the Russian version is easy to find online. If you need I can dm russian pdf to you.
@PoMa yes i want the Russian version, please dm me that, can’t find it anywhere online.