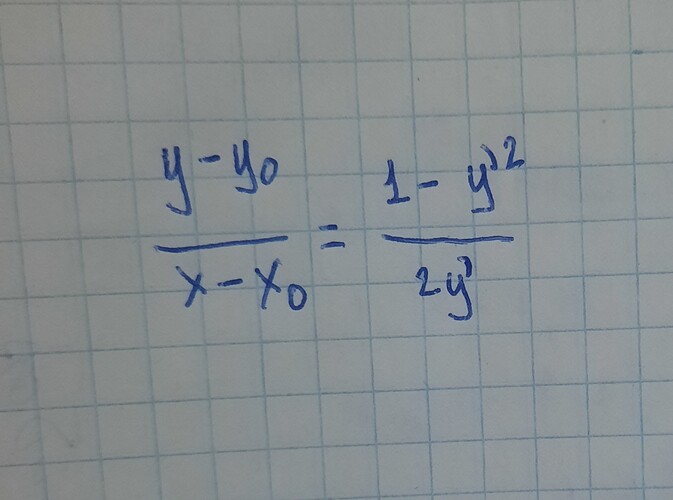Я не особо силён в дифференциальных уравнениях, но у меня есть идея решения для частного случая, где y = kx +b, в таком случае:
\frac {y - y_0}{x-x_0} = \frac {\Delta y}{\Delta x} = k = y'
Находим значение y'
Если подставить это в начальное уравнение, то оно сводится к простому квадратному уравнению относительно y':
3y'^2=1 \Rightarrow y' = \sqrt{\frac 13}
Находим функцию y(x)
Далее подставляем значение производной и в начальные условия, y(x_0) = y_0:
y_0 = x_0 + C \Rightarrow C = y_0 - x_0
И находим конечное уравнение:
y = x + y_0 - x_0
Если подставлять решение в данное, в условии, уравнение, то всё сходится, так что, думаю, это решение является правильным. Тут важно не забыть, что нужно найти решение в общем случае, либо доказать единственность решения
2 лайка
сильно
Я немного засох по дифурам, но кажется это нелинейное дифференциальное уравнение. Если мы перемножим дроби, в конечном итоге у нас будут слагаемое yy', что и является источником нелинейности.
Что можно сказать про нелинейные дифуры? То, что их очень сложно решать в общем случае и решаются они либо графически, либо с помощью каких-то упрощений (как например то, что предложил @ernur045).
Если речь идет про какую-то задачу из естественных наук – скинь условие, очень может быть, что задача решается без этой дифуры. Если же это чисто математический вопрос – я бессилен))
1 лайк
Несложными преобразованиями можно привести диффуру к виду:
y = x\left(\frac{1-(y')^2}{2y'}\right) + \frac{2y_0y' - x_0 +x_0(y')^2}{2y'} = xf(y') + g(y'),
где f, g – какие-то гладкие функции. А диффура выше является уравнением д’Алемберта. Решается оно так.
5 лайков
В продолжении к своему ответу:
Дифференцируя уравнение выше относительно x получаем:
y' = x'\cdot \frac{1-\left(y'\right)^2}{2y'} + x\cdot \left(\frac{1-\left(y'\right)^2}{2y'}\right)' + \\
\ \\
+ \frac{\left(2y_0y' - x_0 + x_0\left(y'\right)^2\right)'2y' - \left(2y_0y' - x_0 + x_0\left(y'\right)^2\right)
\left(2y'\right)'}{\left(2y'\right)^2}.
Вычисляем производную и приводим равенство выше к виду
y' = \frac{1-\left(y'\right)^2}{2y'} + x\cdot \frac{-2y'y''\cdot 2y' - \left(1-\left(y'\right)^2\right)2y''}{4(y')^2} + \\
\ \\
+ \frac{\left(2y_0y'' + 2x_0y'y''\right)\cdot 2y' - \left(2y_0y' - x_0 +x_0\left(y'\right)^2\right)2y''}{4(y')^2}.
Раскрываем скобки и упрощаем уравнение
y' = x_0\cdot \frac{(y')^2 y'' + y''}{2(y')^2} + \frac{1 - (y')^2}{2y'} + x\cdot \frac{-(y')^2 y'' - y''}{2(y')^2}.
Сделаем замену y' = u, домножим на 2u^2 и приведем диффуру к следующему виду:
2u^3 = x_0\left(u^2u' + u'\right) + u - u^3 + x\left(-u^2u' - u'\right) \iff \\
\ \\
\iff u' = \frac{3u^3 - u}{\left(u^2 + 1\right)(x_0 - x)} \iff \frac{dx}{x_0 - x} = \frac{du (u^2+1)}{3u^3-u}.
Интегрируем обе части равенства. Имеем
\int \frac{dx}{x_0 - x} = -\ln|x_o - x| + C,\ \int \frac{du (u^2+1)}{3u^3-u} = \frac{2}{3}\ln\left(1-3u^2\right) - \ln(u) + C.
Приравнивем выражения. Выходит
-\ln|x_o - x| = \frac{2}{3}\ln\left(1-3u^2\right) - \ln(u) + C \iff |x-x_0| = \left(1-3u^2\right)^{-\frac{2}{3}}u^{-1}e^C \iff \\
\ \\
\iff\frac{e^C}{|x-x_0|^{\frac{3}{2}}} = u^{\frac{3}{2}} - 3u^3 \implies \frac{dy}{dx} =u = \sqrt[3]{\frac{e^C}{|x-x_0|^{\frac{3}{2}}} +\frac{1}{2} \sqrt{1-\frac{4e^C}{|x-x_0|^{\frac{3}{2}}}} - \frac{1}{2}}.
Вот таким макаром получаем неявное решение диффуры. Мне кажется явное решение y от x вообще нереально получить.
Пы. Сы. наверняка я где-то ошибся в вычислениях, поэтому надо проверить 
8 лайков
как оказалось, да. интегрировать выражение выше не получится
2 лайка