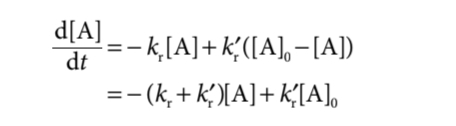
Как это проинтегрировать так, чтобы получить кинетическое уравнение для обратимых реакции Первого Порядка?
Как я уже писал, можно сделать замену переменной, подберем переменную [A]=x+C, чтобы правая часть стала удобной
\begin{gathered}
-(k_r+k'_r)[A]+k'_r[A]_0=-(k_r+k'_r)(x+C)+k'_r[A]_0=-(k_r+k'_r)x+(k'_r[A]_0-(k_r+k'_r)C)\\
\end{gathered}
Если взять \displaystyle С=\frac{k'_r[A]_0}{(k_r+k'_r)}, то получим
\begin{gathered}
d[A]=dx \\
\frac{dx}{dt}=-(k_r+k'_r)x
\end{gathered}
Осталось только проинтегрировать и потом вместо x подставить опять [A]
Можно это делать всё непосредственно уже при интегрировании, т.е. сначала разделить переменные, но потом придется всё-равно в интеграле подобную замену делать
2 лайка
Извините, а как? Интегрировать от нуля до х или как? (Просто х как-то непонятно что)
Что-то не понял, а в чем проблема интегрировать уже по dA/(A-C). С это ведь явно константа, ведь значение А(0) не зависит от хода реакции
Нет такого табличного интеграла
Если A меняется от [A]_0 до [A]_к, то x меняется от [A]_0-С до [A]_к-С, что такое С мы знаем
1 лайк
Ааа, ой. Я подумал раз уж dx/x+a это ln(x+a) то если будет минус, просто заменим плюс на минус
У нас получится ln(A-C/([A]-C)=(k+k’)t. Но мы с этого никак ведь не получим уравнение ниже? (17С.4.)
Ну, то есть к вот этому уравнению я и хотел допрыгать :
Можно так да, но он выводится с помощью того способа, о котором я и писал, обычно его не считают табличным. Есть таблица интегралов от рациональных функций, но её мало кто помнит. Хотя конечно если ты руку набил в интегралах, то уже сразу знаешь как такие \int 1/(ax+b)\, dx вещи интегрируются
Легко получается
4 лайка
Ой, да, тупанул
Большое вам спасибо!