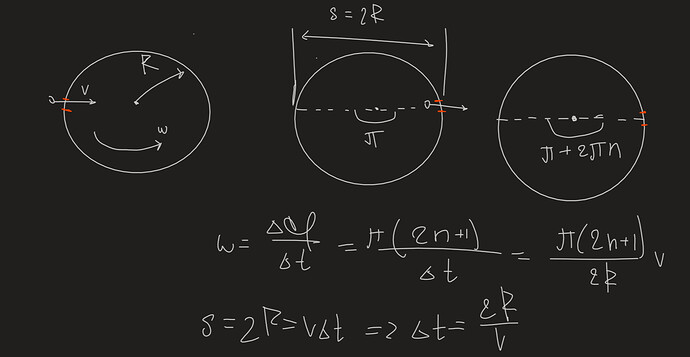Задача 1. (¾Курчатов¿, 2015, 9) Маленький шарик влетает со скоростью v в малое отверстие в стенке полого цилиндра, вращающегося вокруг своей оси (см. рисунок). Радиус R цилиндра много больше толщины его стенок. Скорость шарика перпендикулярна оси цилиндра. Какой должна быть угловая скорость вращения цилиндра ω для того, чтобы шарик вылетел наружу, не испытав соударений? Силу тяжести не учитывайте.
Задачу решил, вышло (пиv)/2R , но в ответе написано ((2n+1)(пи*v))/2R. Можете объяснить почему добавили(умножили) 2n+1?
1 лайк
Я так полагаю к этой задаче прилагается рисунок. Можешь, пожалуйста, его тоже отправить
В твоем случае в цилиндре отверстие преодолела 180 градусов. А тут отверстие может еще и еще больше кругов, значит совершить 540,900 градусов и т.д.
2 лайка
аа простите, если помешал
1 лайк
Ничего, любой может задавать вопросы, и любой может отвечать на них ![]()
1 лайк
вот, я понял что цилиндр может сделать больше кругов, но я не понял как связано количество оборотов с 2n+1
Чтобы мячик мог вылететь, нужно чтобы цилиндр сделал какое-то количество оборотов (1 оборот — 360 градусов или же 2 \pi радиан) и еще полуоборот (180 градусов или \pi радиан)
1 лайк
Чтобы шарик вышел не испытав соударений, он должен выйти с другой стороны цилиндра, двигаясь при этом по прямой линии - преодолевая расстояние 2R с постоянной скоростью v. Значит цилиндр должен как минимум повернуться на 180, но если он повернется на еще 360, 720 положение отверстия будет также оставаться противоположным начальному. Поэтому допустим цилиндр сделал n оборотов, тогда суммарное угловое перемещение 2пn+п=п(2n+1)
5 лайков
ооо спасибо огромное!