Энергия системы из двух шаров и пружины

Физика Механика
1

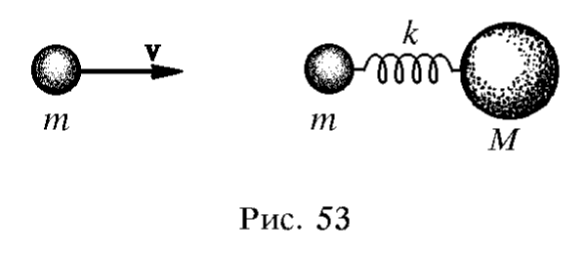
Система состоит из двух шаров с массами m и M, соединенных между собой невесомой пружиной жесткости k (рис. 53). Третий шар массой m, движущийся вдоль оси пружины со скоростью v, претерпевает упругое столкновение с шаром m, как указано на рис. 53. Считая шары абсолютно жесткими, найти после столкновения: 1) кинетическую энергию K движения системы как целого; 2) внутреннюю энергию системы E_{вн}; 3) амплитуду колебаний A одного шара относительно другого. До удара система покоилась, а пружина не была деформирована. Какие шары могут рассматриваться как абсолютно жесткие?
image

Ответ. 1) K = \frac{(mv)^2}{2(M+m)}; 2) E_{вн} = \frac{Mmv^2}{2(M+m)}.

После упругого столкновения третий шар остановится, а шар m в системе получит скорость v. Центр масс системы будет двигаться со скоростью V = \frac{mv}{M+m} (или она не будет постоянной?). Дальше я пытался использовать теорему Кенига:

K = \frac{mv'^2_1}{2} + \frac{Mv'^2_2}{2} + \frac{(mv)^2}{2(M+m)},

где v'_1 и v'_2 скорости относительно центра масс шаров m и M соответственно. Но я тут не понимаю почему они приравнены нулю. Значит ли это, что система движется без колебаний относительно центра масс? Или здесь нужно посчитать энергию в другой системе отсчета?

И насчет второго вопроса: почему эта внутренняя энергия не равна начальной кинетической энергии \frac{mv^2}{2}? Пружина не была деформирована и потенциальной энергии не должно же быть?

2

Насколько знаю внутренняя энергия, это энергия движения системы относительно центра масс + потенциальная.
Внутренняя энергия системы — это потенциальная энергия взаимодействия ее частиц между собой плюс кинетическая энергия движения этих
частиц относительно центра масс системы (внутреннего движения). поэтому и не начальная кинетическая энергия.
В первом вопросе просят энергию движения системы как целого, то есть кинетическую энергию центра масс

4
  1. По ЗСИ движущийся шар (m) обменяется скоростями с покоящимся (m), в Сивухине в этом же параграфе. mv=(m+M)Vцм => Vцм=mv/(m+M).
  2. Кинетическая энергия системы: (m+M)Vцм^2/2 где подставляем Vцм, получаем K=(mv)^2/(2(m+M))
  3. Внутренняя энергия = Полная энергия - Кинетическая энергия. Потерь на тепло нет, значит полная энергия до столкновения перешла в кинетическую энегрию центра масс + внутреннюю энергию системы:
    mv^2/2=(mv)^2/(2*(m+M))+E => E=mMv^2/(m+M)
  4. Амплитуда - макс отклонение достигнется тогда, когда вся внутренняя энергия системы перейдет в потенциальную энергию пружины:
    kA^2/2=E=mMv^2/(m+M) => A=vsqrt(mM/(k(m+M)))
1 лайк