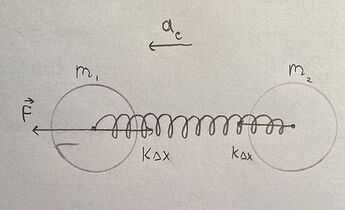
Вообще это можно вывести несколькими способами. Наиболее наглядный и математически строгий это вывод через уравнения движения. Менее наглядный, но логически корректный вывод это вывод через теорему о Вириале через проведение аналогии с обычными гармоническими колебаниями.
1) Уравнения движения тел
В данном способе, мы можем определить изменение внутренней энергии системы через определение движения тел в системе центра масс. Чтобы сделать это, нужно будет решить уравнение движения каждого из тел.
Запишем уравнения движения в системе отсчета центра масс:
m_1 a_1' = F - k\Delta x - F\frac{m_1}{m_1 + m_2}
m_2 a_2' = k\Delta x - F \frac{m_2}{m_1+m_2}
Последние слагаемые являются силами инерции и возникают из-за движения центра масс с ускорением \displaystyle a_C= \frac{F}{m_1+m_2}.
Далее, обозначив координаты тел как x_1, x_2 и выбрав начало координат в центре масс, получим между ними связь как:
m_1 x_1 + m_2 x_2 = 0
В этих координатах уравнения движения можно будет переписать как:
m_1 \ddot x_1 = \frac{m_2F}{m_1+m_2} - kx_1 \frac{m_1+m_2}{m_2} + kl_0
m_2 \ddot x_2 = -\frac{m_2F}{m_1+m_2} - kx_2 \frac{m_1+m_2}{m_1} - kl_0
Эти выражения можно перезаписать в более удобном виде:
\frac{m_1m_2}{m_1 + m_2} \ddot x_1 = -k\left(x_1-\frac{m_2^2F}{k(m_1+m_2)^2}-l_0\right)
\frac{m_1m_2}{m_1 + m_2} \ddot x_2 = -k\left(x_2+\frac{m_2m_1F}{k(m_1+m_2)^2}+l_0\right)
Выражения в скобках в правой части уравнений можно взять за новую переменную, откуда оба уравнения можно перезаписать в виде
\mu \ddot z = -kz
где \mu - приведенная масса нашей системы.
Решая эти дифференциальные уравнения с начальными условиями в виде \displaystyle x_1 =\frac{m_2 l_0}{m_1+m_2}, \dot x_1=0 и \displaystyle x_2 =-\frac{m_1 l_0}{m_1+m_2}, \dot x_2=0 можем получить общее уравнение движения тел в системе центра масс:
x_1 =\frac{m_2 l_0}{m_1+m_2} + \frac{m_2^2F}{k(m_1+m_2)^2} \left(1 - \cos\left(\sqrt{\frac{k}{\mu}}t\right) \right)
x_2 =-\frac{m_1 l_0}{m_1+m_2} - \frac{m_2m_1F}{k(m_1+m_2)^2} \left(1 - \cos\left(\sqrt{\frac{k}{\mu}}t\right) \right)
В нашем случае будут присутствовать затухания колебаний, и поэтому в выражение также следует добавить множитель A(t) перед косинусом, для которого A(0)=1, \lim_{t \to +\infty} A(t) =0, причем A(t) медленно убывает (\displaystyle \dot A(t) \ll \sqrt{ \frac{k}{\mu}}).
В таком случае выражение для полной внутренней энергии можно будет записать как:
E = E_k + E_П = \frac{m_1 \dot x_1^2}{2}+ \frac{m_2 \dot x_2^2}{2} + \frac{k(x_1-x_2-l_0)^2}{2}
Подставляя выражения для x_1, x_2 получим:
E = \frac{m_2^2 F^2}{2k(m_1+m_2)^2} \left(1+A(t)^2 -2 A(t) \cos\left(\sqrt{ \frac{k}{\mu}}t\right) \right)
На первый взгляд, данное выражение кажется очень странным, так как полная энергия у нас зависит от времени. Однако, от этого выражения нам нужно найти только изменение энергии по времени, с помощью которого мы сможем найти потерянную энергию из-за работы сил трения. Взяв производную по времени получим, что:
\dot E = \frac{m_2^2 F^2}{2k(m_1+m_2)^2} \left(2 A(t) \dot A(t) -2 \dot A(t) \cos \left(\sqrt{ \frac{k}{\mu}}t\right) + \sqrt{ \frac{k}{\mu}} A(t) \sin \left(\sqrt{ \frac{k}{\mu}}t\right)\right)
Можно заметить, что так как \displaystyle \dot A(t) \ll \sqrt{ \frac{k}{\mu}}, то при нахождении полной потери (интегрировании этого выражения) произойдет многократное усреднение по периоду колебаний. Таким образом, слагаемые с синусами и косинусами отпадут и в итоге потеря энергии будет:
\Delta E = \frac{m_2^2 F^2}{2k(m_1+m_2)^2}
Добавляя к этой энергии энергию конечного растяжения пружины, получим выражение для полного прироста внутренней энергии:
E = \frac{m_2^2 F^2}{k(m_1+m_2)^2}
2) Гармонические колебания и теорема о Вириале
Как было показано предыдущем выводе, движение тел в нашем случае сводится к простому уравнению гармонических колебаний, т. е. \mu \ddot z = -kz. Для такого уравнения видно, что в нашем случае сила F \propto z^1, а значит потенциальная энергия U \propto z^2.
Тогда используя теорему о Вириале (см. Вириал — Википедия) можно получить, что
2\langle T\rangle =n\langle U\rangle = 2\langle U\rangle \rightarrow \langle T\rangle=\langle U\rangle
То есть полная энергия системы будет:
E =\langle U\rangle + \langle T\rangle = 2 \langle U\rangle