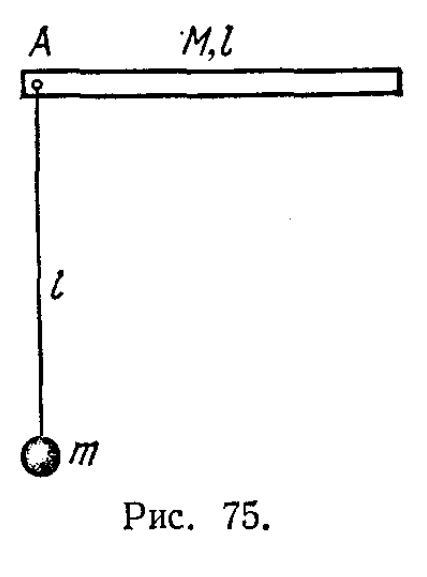
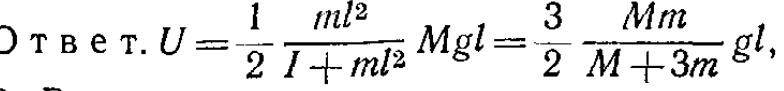- Твердый стержень длины и массы М может m вращаться вокруг горизонтальной оси А, проходящей через его конец (рис. 75). К той же оси А подвешен Рис. 75. математический маятник такой же длины и массы т. Первоначально стержень занимает горизонтальное положение, а затем отпускается. В нижнем положении происходит идеально упругий удар, в результате которого шарик и стержень деформируются, и часть кинетической энергии переходит в потенциальную энергию деформации. Затем деформация уменьшается, и запасенная потенциальная энергия вновь переходит в кинетическую. Найти значение потенциальной энергии деформации U.
Вот мое решение → потеницальная энергия переходит в вращательную: Iw^2=2mgl. Еще по закону сохранения момента импульса: Iw=mVl-Iw2.
Еще по закону сохранение энергий: Iw^2/2=mu^2/2+Iw2^2/2+U. Отсюда я нашел функцию U(w2) и взял производную. Нашел Umax и у меня вышло U=Mgl((m+M)/(M+3m)).
А ответ этой задачи
Мне кажется у меня ошибка в арифметике
Сперва распиши ясно насколько изменится потенциальная энергия стержня в начале.
U_{max} можно найти и через производную, но удобнее сделать по другому. До некоторого момента удар можно принять за неупругий, когда оставшаяся энергия перейдет в энергию деформации. В этот момент шарик и стержень перестанут действовать друг на друга.
Я увидел что я неправильно расписал изменение потенциальной энергии. У меня вопрос возник почему можно считать в начале за неупругий?
Точнее надо было сказать, что сам удар упругий, но упругие эффекты не проявляются сразу. Пока у стержня есть скорость относительно шара, абстрактная “пружинка” между ними будет сжиматься и набирать потенциальную энергию. Когда они перестанут двигаться друг относительно друга, “пружинка” растянется, и эта энергия перейдет в кинетическую.
Все я понял спасибо за ответ