В этой теме обсуждаем задачи oblast олимпиады 2021 года
Это обсуждение публикации https://olympiads.bc-pf.org/physics/oblast/2021/11
Это обсуждение публикации https://olympiads.bc-pf.org/physics/oblast/2021/11
Что дальше делать? Задача с области 11 класса.
Среди трудов Уильяма Томсона нашли манускрипт с pV-диаграммой для идеального газа. На диаграмме был нарисован циклический процесс в виде треугольника KML, где угол при вершине M был прямым. Точка F изображенная на рисунке лежит на середине стороны KL. В данной точке, теплоемкость многоатомного газа равно нулю. Зная только точки M и F, восстановите данный цикл. Объем в точке K меньше чем в L. (Можно использовать только циркуль и линейку без делений)
Дальше смотрел решение к этой задаче,но все равно не понял нихрена:
1 лайк
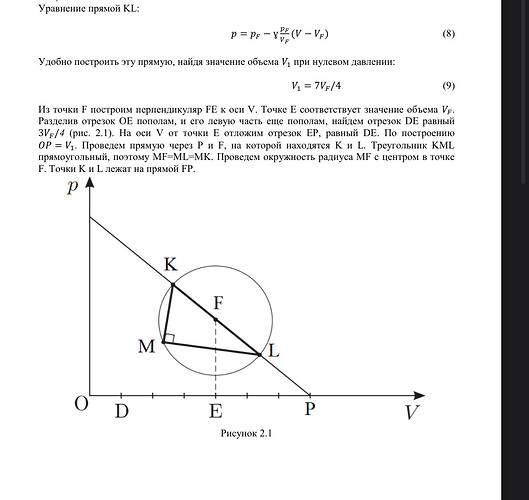
Зная, что в точке F теплоемкость газа равна нулю можно сказать, что в ней график цикла касается адиабаты. Тогда так как прямая KL должна касаться адиабаты, то ее наклон будет как у адиабаты, откуда можно получить уравнение прямой приведенное в решении. Далее, в решении они отмечают точку P, лежащую на прямой и соответствующей объему 7V_F/4. Это можно сделать с помощью построения перпендикуляра из F к OV и построением серединного перпендикуляра к отрезку OE и его половинному отрезку. С помощью этого можно получить длину в V_F/4, отложить три таких расстояния по прямой с помощью циркуля от точки E, найти точку P, и начертить прямую FP.
Кроме того, для прямоугольного треугольника середина гипотенузы является центром описанной вокруг него окружности, из чего следует, что FM=FL=FK, откуда относительно F можно построить окружность с радиусом FM и получить точки K и L там где окружность пересекается с прямой.
Если не знаешь как строить серединный перпендикуляр к отрезку, то тык, и если не знаешь как построить перпендикуляр к прямой из точки, то тык
2 лайка
А каким образом получить это уравнение прямой?
Это уравнение,вид которого имеет ax+by+c=0?
Это просто уравнение прямой проходящей через точку F с определенным наклоном. Его можно записать как
y = y_0 +k(x-x_0)
Наклон ты найдешь из наклона адиабаты
\frac{dp}{dV}=-\gamma \frac{p}{V}
2 лайка
Боже,спасибо большое за помощь.А в самом решении другое правильно найдено? Я попытался обойти дифференцирование,т.к пока это делать не умею от слова совсем.А вопрос про формулу “dpV+pdVp…” .Она как выводится? Нам в школе ее дали,сказав,что на ЕНТ попадаются задачи ,в которых сначала идет изменение давления,а потом объема.И она есть,кажется,в Кронгарте 10 класса 2010-2014 года без вывода также.
1 лайк
Да, все верно
Ее можно получить рассмотрев изменение для уравнения \nu RT = PV. При небольшом изменении температуры, давления и объема в силу уравнения должно быть
\nu R(T+\Delta T) = (P+\Delta P)(V+\Delta V)
Откуда используя предыдущее уравнение получим:
\nu R \Delta T = V\Delta P+P\Delta V+\Delta P \Delta V
так как \Delta P, \Delta V это малые величины, то слагаемым \Delta P \Delta V можно пренебречь и получается выражение \nu R \Delta T = V\Delta P+P\Delta V
6 лайков
« На столе лежит прямоугольная рамка с током / имеющая
форму прямоугольника со сторонами а и b, ориентированными вдоль осей х и у соответственно. Рамка находится в магнитном поле с составляющими (0, Ву,8 By).
- Покажите, что величина момента магнитных сил, действующих на рамку в описанном случае, равна М = IB,S, где S - площадь рамки. Вокруг какой оси этот момент стремится повернуть рамку?
- Покажите, что величина момента магнитных сил, действующих на произвольной формы рамку с током в магнитном поле, равна М = IB|S, где B|
- составляющая магнитного поля, лежащая в плоскости рамки, S - площадь рамки.
c) На какой угол от вертикали отклонится такая рамка с током (см. рис) в вертикальном магнитном поле
B = 0,1 л? Все звенья рамки изготовлены из одинаковой проволоки. ABCD - квадрат со стороной а = 20 см.
Внутренние звенья соединяют середины сторон. Масса единицы длины проволоки р = 40 г/м. Ток в рамке 1 = 0,1А. Ускорение свободного падения принять равным g = 9,8 м/с2»
Хочу попросить о наводке для решения задача,хотя понимаю,что в самих вопросах ее явно указали.
Во-первых,что за сила Fz?( не совсем понимаю смысл индекса,который только сбивает с толку) Правильно ли предполагать ,что на сторону AD будет действовать сила,которая не будет создавать момент сил,а лишь деформировать саму рамку? А на рамку будут действовать две одинаковые по модулю ,но разные по направлению силы,которые будут образовывать «пару сил»?Как правильно направить положительную нормаль? Может есть какой более рациональный метод решения задачи?
2 лайка
Это просто проекция силы на ось z
Да затем считаешь момент этой пары сил
Ну это повлияет на знак силы, но модуль момента сил у тебя выйдет таким же вне зависимости от того куда ты направишь эту нормаль
2 лайка
А что за ось z? По условию даны оси x и y.Или самому ввести ее надо?
Остановись немного и подумай:
Сила действующая на проводник в магнитном поле:
\vec{dF}=I(\vec{dl}\times \vec B) =Idl(\hat i\times\vec B)\Rightarrow \vec F=\int Idl(\hat i\times\vec B)
Здесь можно ввести единичный вектор в направлении течения тока \hat i \rightarrow\vec{dl}=dl\hat i
Отсюда ясно, что вектор силы сонаправлен с вектором (\hat i\times \vec B), a проекции вектора (\hat i\times \vec B) можно посчитать через векторное произведение:
(\hat i\times \vec B)=\begin {pmatrix}\hat x& \hat y &\hat z\\\ i_x& i_y & i_z\\ B_x& B_y& B_z \end {pmatrix} =\hat x(i_yB_z- i_z B_y)+\hat y(i_zB_x-i_xB_z)+\hat z (i_xB_y-i_yB_x)
так как B_z=i_z=0, значит останется только компонента по оси z:
(\hat i\times \vec B)=\hat z (i_xB_y-i_yB_x)
Поэтому сила в этом случае будет действовать по оси z
8 лайков