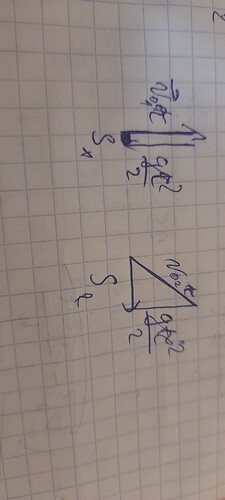1.10. Два тела бросили одновременно из одной точки: одно - вертикально вверх, другое под углом \phi =60\degree к горизонту. Начальная скорость каждого тела v=25м/с. Найти расстояние между телами через t =1,70 с.
1.11. Два шарика бросили одновременно из одной точки в горизонтальном направлении в противоположные стороны со скоростями v=3,0м/с \space и \space v=4,0м/с. Найти расстояние между шариками в момент, когда их скорости окажутся взаимно перпендикулярными.
Не могли бы вы помочь с решением именно через относительность(в ютубе через функцию)
Вектор перемещения равноускоренно движущегося тела, как тебе должно быть известно, есть
Нарисуй графически эту сумму векторную, без перехода в относительные системы.
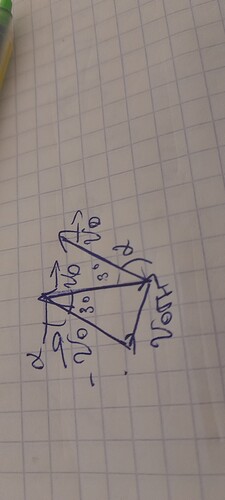
Вот я рассписал для 1 задачи кстати данное уравнение для обейх тел рассписать?
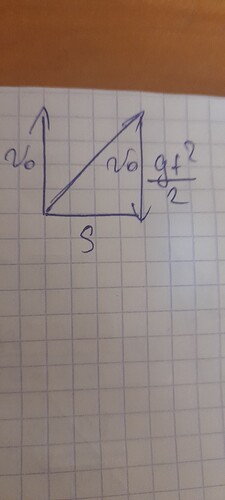
Для 2 задачи полкчилось
У 1 рисунка не совсем понятно. А вот второй рисунок уже больше похож на правду. Но ты в неправильных местах указал v_{01}t и v_{02}t)) Перечитай условие и определи направления этих векторов по-нормальному
Ага. Теперь по геометрическим соотношениям определяешь время t из условия перпендикулярности, и тогда получится ответ
Спасибо, а что делать с первой задачей я так и не понял:(
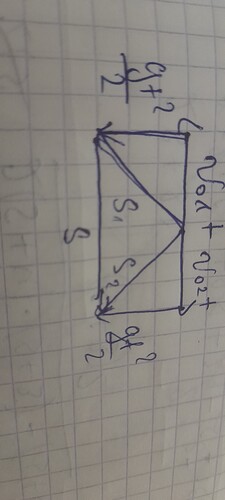
Проставь вектора, и укажи все компоненты суммы (и ориентируй фотки как надо). Сделай это для двух тел, и находи разность результирующих векторов \Delta\vec s_1 и \Delta\vec s_2.
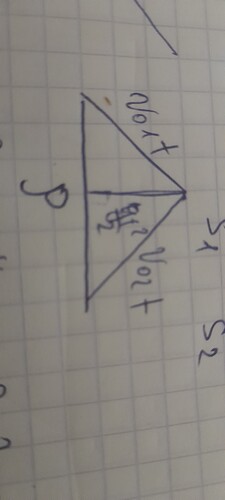
Чтото я опять не понял:( для брошенного вертикально вверх тела перещение равно точке(типо откуда оно было брошено туда и упало) а для второго тела вот так?
Так нигде и не было сказано, что через 1.7 с тело упадёт на землю. Нарисуй треугольники для более общего случая.
И, напоминаю, ориентируй фото вот так:
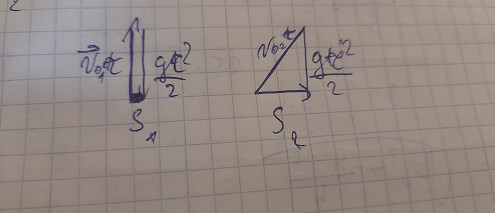
Иначе пользователям настольной версии сайта тяжело смотреть на изображения
Ааа я просто не понял что вы имели ввиду про фотографию, теперь буду знать
Скажу честно я так и не понял пожалуйста моэете написать ответ
Я вижу, что ты совсем затрудняешься графический способ применять. Всегда начинай читать теорию в таких случаях, прежде чем возвращаться к этой задаче. Я бы порекомендовал начать с параграфа 1.11 Мякишева и его упражнений по кинематике.