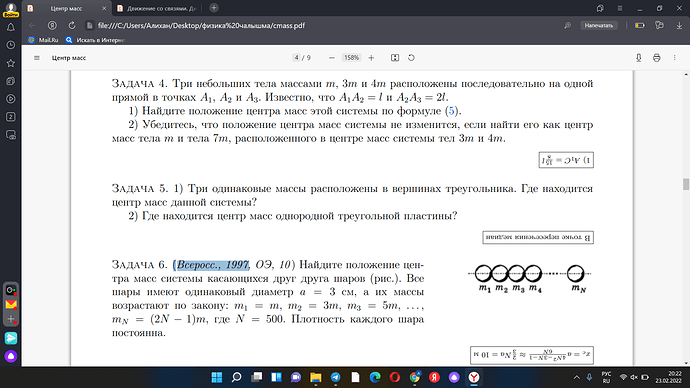
Найдите положение центра масс системы касающихся друг друга шаров (рис.). Все
шары имеют одинаковый диаметр a = 3 см, а их массы возрастают по закону: m_1 = m, \ m_2 = 3m, \ m_3 = 5m, \ \dots, m_N = (2N − 1)m, где N = 500. Плотность каждого шара постоянна.
1 лайк
Расстояние между центрами двух соседних шаров — это сумма радиусов двух шаров. Поскольку плотность каждого шара постоянна, для каждого отдельного шара центр масс будет находиться в центре шара. Поэтому можно все представить, как ряд из 500 точек, которые имеют массу (2N-1)m и выстроены на расстоянии 2r друг от друга.
Возьмем за 0 координату центра самого первого шара. Существует центр масс, который находится на расстоянии x от этого нуля. Для центра масс будет справедливо следующее выражение:
mx + 3m (x-2r) + 5m (x-4r) + \dots + 997m (x-994r) + 999m (x-998r) = 0
То, как изменяются массы, нам дано. Выражение в скобках по модулю равно расстоянию от конкретной точки до центра масс. Можно увидеть зависимость — каждое слагаемое выражается следующим образом в зависимости от N:
(2N-1) \cdot m \cdot (x-2(N-1)r) = m (2N-1) (x+2r - 2Nr)
Тогда вся сумма выражается так (я сразу раскрыл скобки):
\sum_{N=1}^{500} m (2Nx + 6Nr - 4N^2r - x - 2r) = 0
Постоянные значения (r, \ x, \ m) можно вынести за знак суммы и останется следующее:
2mx\sum_{N=1}^{500}N + 6mr \sum_{N=1}^{500}N - 4mr \sum_{N=1}^{500} N^2 - 500mx - 1000mr = 0
Зная, что \displaystyle\sum_{r=1}^{n} r = \frac{n (n+1)}{2} и \displaystyle\sum_{r=1}^{n} r^2 = \frac{n(n+1)(2n+1)}{6} (если не знаем, можно быстро вывести), получим
500^2x = 1500 + 250 \cdot 501 \cdot (2002 - 9)
Отсюда выходит, что x = \pu{998.499 cm} \approx \pu{10 m}.
6 лайков
у физиков тем итак мало, ты еще и забираешь
1 лайк