2.1.60 савченко

Физика
1

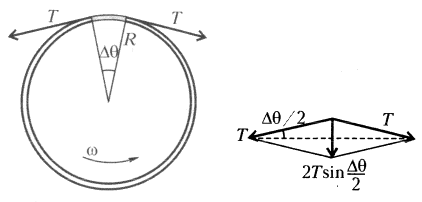
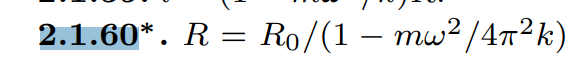Из тонкого резинового жгута массы m и жесткости k сделали кольцо радиуса R0. Это кольцо раскрутили вокруг его оси. Найдите новый радиус кольца, если угловая скорость его вращения равна ω.

image
image1120×68 10.6 KB

Я не могу понять почему ответ вот такой. Я попробовал сделать так я приравнял силу Гука на центробежную силу

F_U=k\Delta x

где 2\pi(R-R_0)

F_U=2\pi k(R-R_0)
F_{цб}=mω^2R_0

И вышел ответ

R=\frac{R_0(mω^2-2\pi k)}{2\pi k}
1 лайк
2

image
Попробуй рассмотреть маленький кусочек массы кольца равный m` = m * R * delta a / (2 pi R)=
= m * delta a / (2 pi )
на картинке T = Fu

1 лайк
3

То есть у меня центростремительная сила будет

F_цб=\frac{m'ω^2da}{2\pi}

А сила Гука чему будет равно?
Ну типа она равно

F_{Uт}=2Tsin\frac{\alpha}{2}

И если подставим значение Т то

F_{Uт}=4\pi kda\cdot d(sin\frac{\alpha}{2})

правильно?

Где мы возьмем пределы маленького кусочка от R_0 до R, а пределы синуса половину угла от 0 до 2\pi.

1 лайк
4

Тут не m` ,а просто m
И там альфа

Сила гука для малого отрезка это у тебя и есть T. А втором уравнении ты выражаешь проекцию сил Гука на ось направленную на ось окружности.

Приравняй \vec{F_{цб}} к 2\vec T_x

Альфа-малый угол. sin(\alpha/2) \approx \alpha/2

Теперь чтобы найти T найдем связь между T и F_u
T=k_n\frac{2\pi(R-R_0)}{n} и \frac{1}{k}=\frac{n}{k_n} где k_n-жесткость отрезка кольца
T=F_u

1 лайк
5

А зачем нам n?

1 лайк
6

Мы разделили кольцо на n равных отрезков и рассматриваем момент когда этот отрезок в состоянии покоя.
Используем n чтобы доказать, что F_u=T

1 лайк
7

Если приравнивать F_{цб}=2T_x

\frac{mω^2Rd\alpha}{2\pi}=\frac{4\pi k(R-R_0)d\alpha}{2}

Я правильно написал формулу?

3 лайка
8

Ты забыл умножить на два правую формулу

2 лайка
9

Теперь правильно?

10

Правильно

3 лайка
11

Но у меня вышел ответ

R=\frac{R_0}{(1-\frac{mω^2}{4\pi^2k})}

Но ответ

R=R_0(1-\frac{mω^2}{4\pi^2k})
3 лайка
12

Нет, твой ответ совпадает с ответом в задачнике.
image
Есть ли какие либо еще затруднения? @Sagi_Sabyrtai

3 лайка
13

Простите, возник вопросы по задаче. Почему мы силу натяжения всего кольца, равную 2П(R-R0) приравниваем к силам натяжения, действующей на маленький участок колца