Начальная скорость выделения O2 при действии фермента на субстрат была измерена для ряда концентраций субстрата:
Определите константу Михаэлиса данной реакции.
Как решать такие задачи как 23-13 и 23-14
Я брал максимальную скорость как 16,6 подставлял под уравнение Михаэлиса концентрации брал как (0.05-0.017) и так нашел 4 Км взял среднее их значение но далеко не вышло
Ответы:
23-13
Км= 1* 10^-2
23-14
Км= 4.0* 10^-2 ; r max=4.4*10^-5
2 лайка
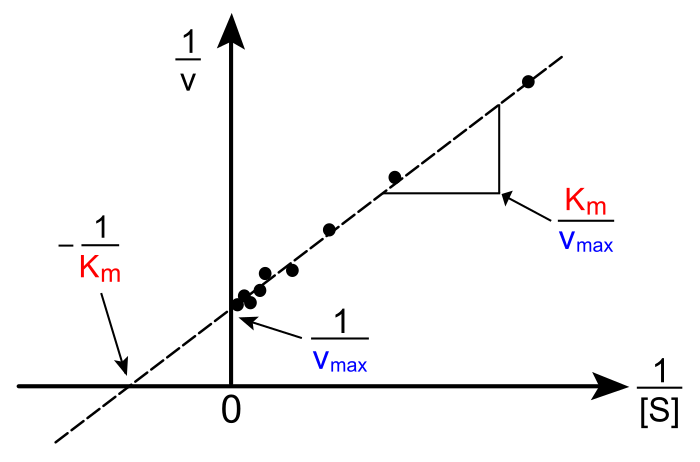
Как видите в 23-14 показан линейный график. Вам нужно понять какой вид имеет это линейное уравнение. По координатам понимаем что вид такой: \displaystyle r=m\cdot\frac{r}{\ce{[S]}}+b, и не забывайте про единицы измерения. Это уравнение было выведено из уравнения Михаэлиса-Ментен, так что вы можете сами понять что такое m и b, если попробуете вывести такую линейную зависимость. Вообще, рекомендую прочитать теоретическую часть 23 главы, там об этом сказано. И возможно похожая задача еще решалась в примерах в начале.
2 лайка
Координаты Лайнуивера - Берка
r =r max - Km * r/[S]
Да в примерах есть похожая задача,но решение я совсем не понял, как они нашли максимальную скорость, и какие точки они берут.
1 лайк
Мы примерно приблизительно берём значения координат? ( Если так то выходит )
2 лайка
Вы умеете считать наклон y=kx+b ? Плюс находить intercept ? Если можете то проблем не должно быть, а так надо посмотреть как это делать
Я не мастер наклон и в олимпиадах где время урезано беру тупо 2 точки и так нахожу
P.S ( С такой линией как тут без явных точек я бы просто систему составил)
2 лайка
Там есть 4 варианта(или больше):
- Самый легкий. Заходишь в режим statistics на белом калькуляторе(Casio FX-991 EX). Там выбираешь линейную функцию, вставляешь координаты всех точек, а затем нажимаешь на OPTN->Regres. Calc., и он выдаст значение наклона и игрик-пересечения.
- Посчитать параметры используя Метод наименьших квадратов.
- Самому руками поставить точки на графике, а затем провести best fit line, а затем взять любые две точки на линии и посчитать через них наклон \left(\displaystyle наклон=\frac{y_2-y_1}{x_2-x_1}\right)
- Можно использовать онлайн штуки по типу desmos.com , но на олимпиаде конечно вам не дадут их использовать
5 лайков
Как бы вы составили систему?
1 лайк
Линейкой провел бы : 3,3 и 2,6, Проведите пж линейкой через разные r, я не уверен, но должно выйти
Точки невнятные, я так еще не работал, поэтому просто составил бы систему
1 лайк
Да 3:3 и 6:2 и 9:1 Сейчас пробую мнк ( ладно завтра дорешаю сегодня прям никак )
2 лайка
Я забыл написать о том что понял как решать такие задачи. с помощью мнк y=kx + a. a это макс скорость, k это наклон r max/ km. Это так потому что можно вывести линейное уравнение Лайнуивера Берка там х это 1/[S] , y это 1/r.
Только в задаче 23-14 немного корявый график и точных точек не видно, это нормально будет если я скипну эту задачу?
1 лайк
23-14 в итоге соотношения не 3:3, 6:2, 9:1 брал эти значения и не вышло, провел линейкой и понял что явно не такие соотношения. 23-13 вышло
1 лайк
Мне кажется на олимпиаде такой не дадут
3 лайка
В 23-14 у тебя координаты другие. Вроде есть два вида линеаризации, как я помню из теоретической части учебника.
И точки можешь взять примерно на глаз, линейкой там поработать
Хорош. Ну ты хоть заспойлерил бы, человек попытался бы
1 лайк
сорри я забыл, надеюсь он не увидел
1 лайк
Не увидел
1 лайк
А как вы поняли что это другие координаты, и нужно брать другой тип линеаризации?
1 лайк
Вот показали что игрик координата это r\cdot 10^5, а размерность игрик координаты моль\cdot л^{-1}\cdot с^{-1}
Соответственно, икс-координата это \frac{r}{\ce{[S]}}\cdot10^4 с размерностью с^{-1}.
Например, если при \ce{[S]}=1\ моль\cdot л^{-1} , r=2\ моль\cdot л^{-1}\cdot с^{-1}, то
y=r\cdot10^5= 2\ моль\cdot л^{-1}\cdot с^{-1}\cdot10^5=2\cdot10^5 \ моль\cdot л^{-1}\cdot с^{-1}
x=\frac{r}{\ce{[S]}}\cdot10^4=\frac{2\ моль\cdot л^{-1}\cdot с^{-1}}{1\ моль\cdot л^{-1}}\cdot10^4=2\cdot10^4\ с^{-1}
Попробуй теперь вывести выражение для наклона и y-пересечения для такой линейной зависимости.
Еще, у нас график стремится вниз, а не вверх, это означает что наклон отрицательный: y=mx+b,\ m<0.
График Лайнвивера-Берка имеет положительный наклон, поэтому линия стремится вверх:
\frac{1}{r}=\frac{K_M}{r_{\text{max}}}\cdot\frac{1}{\ce{[S]}}+\frac{1}{r_{\text{max}}}
\\
m= \frac{K_M}{r_{\text{max}}}>0, потому\ что\ K_M>0\ и\ r_{\text{max}}>0
8 лайков
У меня вышла эта задача когда я прям точно измерил линейкой что они по абсциссе берут за 3 и тд, нашел тангенс альфа этого треугольника и прям точно вышло
1 лайк