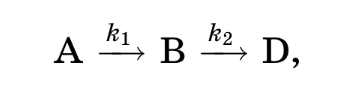
В этой схеме как-то вывели время где В имеет максимальную концентрацию.
t_{max}=\frac{ln(\frac{k_2}{k_1})}{k_2-k_1}
Можете объяснить откуда вышла эта формула?
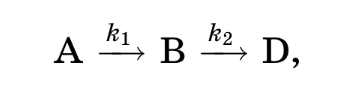
В этой схеме как-то вывели время где В имеет максимальную концентрацию.
t_{max}=\frac{ln(\frac{k_2}{k_1})}{k_2-k_1}
Можете объяснить откуда вышла эта формула?
вы можете показать свой ход решения
Я в общем вывел концентрацию [B] и у меня вышло:
[B]=\frac{[A]_0k_1}{k_2-k_1}(e^{-k_1t}-e^{-k_2t})
Дальше не знал что делать.
Так как нам нужно найти время при котором конц. В будет максимальна, вы можете взять производную по времени уравнение для B и приравнять это выражение к нулю
Какое условие должно быть для максимальной концентрации ?
Я дальше попробовал решить взяв [B]_{max}=[A]_0 и вышло уравнение:
Дальше это уравнение не смог решить
А как это связано с друг-другом?
Получается если смотреть график концентрации В от t, это будет выглядеть как парабола и наклон в максимальной точке будет равен нулю?
d[B]/dt будет равен нулю, поскольку наклон при максимальной концентрации равен нулю
понял спасибо @M3ndeII
В общем случае следует четко понимать, что условие “\dfrac{dy}{dx} = 0 в какой-то точке x^*” может и ничего не говорить про точку максимума (речь идет про абсолютный максимум). Иногда бывает такое, что максимум функции находится на границе области определения функции, хотя внутри области определения есть точка(-и) в которой(-ых) производная функции равна нулю. Иногда бывает такое, что максимум функции вообще находится в точке, в которой производная функции не может быть определена. Иногда это условие может указывать на точку минимума, или вообще ни на максимум, ни на минимум (речь идет про локальный максимум/минимум).
Я все это к тому, что по хорошему надо смотреть на поведение самой функции, и ни в коем случае не бросаться плотно закреплять у себя утверждение “чтобы найти максимум функции, достаточно просто взять производную функции и приравнять к нулю”, ибо это может привести к беде в будущем, при столкновении с другими задачами, которые будут требовать нахождение точки максимума. Если трудно представить поведение функции, то можно воспользоваться разными тестами для дифференцирования между точками локального минимума/максимума (к примеру, смотреть на знак второй производной, если это возможно), смотреть на границы области определения (если они вообще имеются), и так далее.
а чеб вы не возьмете и не посмотрите? desmos.com
или просто правило произведения + производная e^x.