Круговой контур на поверхности магнетика

Физика Электромагнетизм
1

изображение
изображение2048×384 125 KB

2

У тебя уже есть какие-то попытки решения задачи?

3

Думаю кольцо можно представить в виде магнитного диполя[ вот только я не смог((((] и написать циркуляция вектора H

изображение
изображение2048×1536 549 KB

1 лайк
5

Свою идею с магнитными диполями ты хорошо начал, но в этой задаче решение идёт через метод изображений. Эта задача примерно аналогична задаче электростатики об изображении точечного заряда рядом с диэлектрической плоскостью. Решение ниже

Введу магнитный момент \overrightarrow m, который создаёт поле реального кругового витка (см. рисунок ниже).

image
image767×566 6.15 KB

Тогда внутри магнетика располагается момент-изображение \overrightarrow{m'}, причём:

  1. Граница раздела вакуум-магнетик находится ровно посередине между моментами \overrightarrow m и \overrightarrow{m'}.
  2. Вектор \overrightarrow{m'} сонаправлен \overrightarrow m (это дело выбора направления координат, так что это необязательный пункт)
  3. Создаваемые ими магнитные поля рассматриваются только в вакууме.

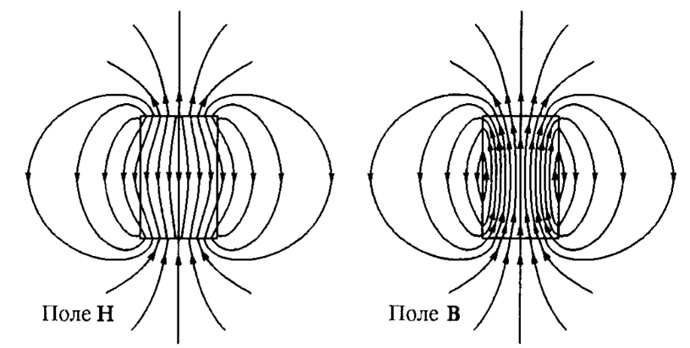
Как описать магнитное поле внутри магнетика? Понятно, что в магнетике силовые линии магнитного поля сгущаются, причём общая форма этих линий внутри магнетика несильно отличается от силовых линий в этой же окрестности в вакууме. Для примерного понимания прикрепляю картинку:

image
image816×412 45.8 KB

Таким образом, нужно ввести третий магнитный момент \overrightarrow{m''}, который:

  1. Расположен там же, где и реальный круговой виток.
  2. \overrightarrow{m''} сонаправлен \overrightarrow m.
  3. Он описывает магнитное поле внутри магнетика (\overrightarrow m и \overrightarrow{m'} не учитываем).

С учётом всего вышеперечисленного приступим к решению задачи. Для этого напишем выражения, описывающие величину и направление магнитного поля на поверхности магнетика и запишем граничные для них условия. Пусть выбранная точка будет на расстоянии \vec r от реального кругового витка и \vec{r'} от изображения, причём

|\vec r| = |\vec{r'}|=r \newline (\vec r ·\hat x) = -(\vec{r'}·\hat x) \newline (\vec r ·\hat y) = (\vec{r'}·\hat y)
\vec m = m \hat x \newline \vec{m'} = m'\hat x \newline \vec{m''} = m''\hat x

Здесь \hat x и \hat y – базисные векторы осей x и y (см. первый рисунок)

Магнитное поле трёх диполей описывается выражениями

\vec B = \frac{\mu_0}{4\pi} (\frac{3(\vec m·\vec r)\vec r}{r^5}-\frac{\vec m}{r^3}) = \frac{\mu_0}{4\pi} (\frac{3m(\vec r·\hat x)\vec r}{r^5}-\frac{m \hat x}{r^3})=\frac{\mu_0m}{4\pi r^3} (\frac{3(\vec r·\hat x)\vec r}{r^2}-\hat x)
\vec{B'} =\frac{\mu_0}{4\pi} (\frac{3(\vec{m'}·\vec{r'})\vec{r'}}{r^5}-\frac{\vec{m'}}{r^3})= -\frac{\mu_0m'}{4\pi r^3} (\frac{3(\vec r·\hat x)\vec{r'}}{r^2}+\hat x)
\vec{B''} =\frac{\mu_0}{4\pi} (\frac{3(\vec{m''}·\vec{r})\vec{r}}{r^5}-\frac{\vec{m''}}{r^3})= \frac{\mu_0m''}{4\pi r^3} (\frac{3(\vec r·\hat x)\vec{r}}{r^2}-\hat x)

Теперь запишем это в проекциях на x и y:

B_x=\vec B · \hat x = \frac{\mu_0m}{4\pi r^3} (\frac{3(\vec r·\hat x)^2}{r^2}-1)
B'_x=\vec{B'} · \hat x =\frac{\mu_0m'}{4\pi r^3} (\frac{3(\vec r·\hat x)^2}{r^2}-1)
B''_x=\vec{B''} · \hat x = \frac{\mu_0m''}{4\pi r^3} (\frac{3(\vec r·\hat x)^2}{r^2}-1)
B_y = \vec B · \hat y = \frac{\mu_0m}{4\pi r^3} ·\frac{3(\vec r·\hat x)(\vec r·\hat y)}{r^2}
B'_y=\vec{B'} · \hat y= -\frac{\mu_0m'}{4\pi r^3}·\frac{3(\vec r·\hat x)(\vec r·\hat y)}{r^2}
B''_y=\vec{B''} · \hat y = \frac{\mu_0m''}{4\pi r^3} ·\frac{3(\vec r·\hat x)(\vec r·\hat y)}{r^2}

И наконец-то, запишем граничные условия. Для условия сохранения нормальной составляющей вектора \vec B (\nabla· \vec B = 0 либо B_{1n}=B_{2n}):

B_x+B'_x=B''_x \newline m+m'=m''

И непрерывности тангенциальной составляющей вектора \vec H (\oint{\vec H·d\vec l = 0 } при отсутствии токов на поверхности магнетика; H_{1t}=H_{2t}):

\frac{B_y+B'_y}{\mu_0} = \frac{B''_y}{\mu \mu_0} \newline m-m'=\frac{m''}{\mu}

Таким образом:

m''=m \frac{2\mu}{\mu +1} \newline m' = m\frac{\mu-1}{1+\mu}

Когда провод лежит на магнетике, то его поле равно полю эквивалентного кругового витка с m\rightarrow m+m'=m \frac{2\mu}{\mu +1} в вакууме и m \rightarrow m'' = m \frac{2\mu}{\mu +1} в магнетике. Окончательно:

\vec B = \vec{B_0} \frac{2\mu}{\mu +1}
9 лайков
7

Спасибо большое!!!

8

А откуда вы нашли это выражение?

9

Эта формула выводится во многих теоретических книжках. В Сивухине есть только вывод для электрического диполя (это уравнение отличается от уравнения для магнитного диполя только заменой \frac{\mu_0}{4\pi} → \frac{1}{4\pi \epsilon_0} и \vec m → \vec p, где \vec p=q\vec l - электрический момент). В Purcell есть вывод с использованием понятия векторного потенциала. Для начала можно прорешать этот листок, в нём вывод формулы идёт только с использованием закона Био-Савара-Лапласа и некоторых соображений.

4 лайка
10

Спасибо!

В Purcell есть вывод с использованием понятия векторного потенциала.

Можете сказать номер страницы?

11

параграф 11.3, 531 страница

2 лайка