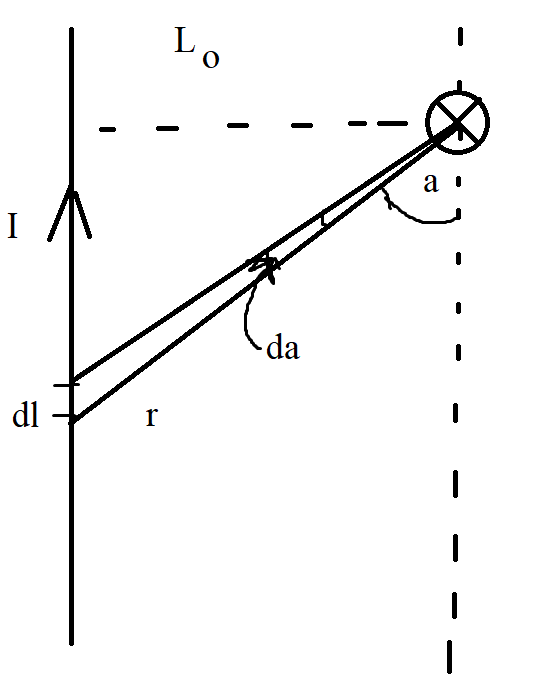2.238
B с каждого провода нашёл с помощью формулы B=(u0I/4πd)×(sina+sinb)
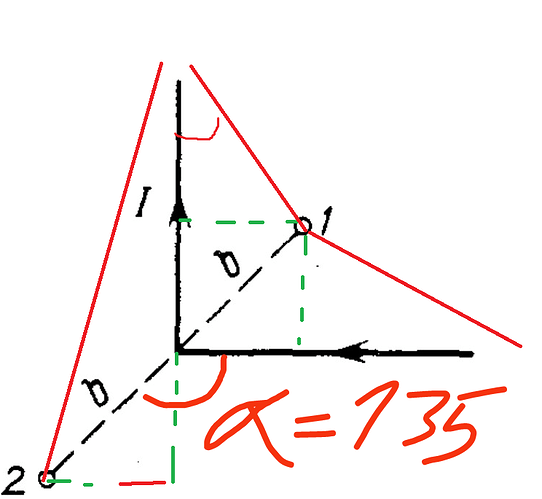
a у нас 135°
b у нас 0°
Направление у них одинаковое, поэтому суммируем.Ответ неправильный.
Помогите найти ошибку.
3 лайка
Я бы больше советовал использовать формулой из закона (Био-Савара-Лапласса) для определения магнитной индукции каждой точки уравнением
\displaystyle B=\frac{{\mu}{\mu_0}I}{4{\pi}L_0}(\cos{\alpha_1}-\cos{\alpha_2})
Где L_0 - это кратчайшее расстояние до провода
Это воображения этой формулы, нужно понять откуда она исходит и что она из себя представляет. Сам закон представляет о том, что благодаря нему, можно определить модуль вектора магнитной индукции в любой точке магнитного поля при постоянном электрическом токе в проводе.
Сама формула выглядит вот так:(дальше идет ответ на вопрос: что и зачем за закон Био-Савара-Лапласса):
B=\frac{\mu\mu_0}{4\pi}I\int\frac{\sin{\alpha}}{r^2}dl
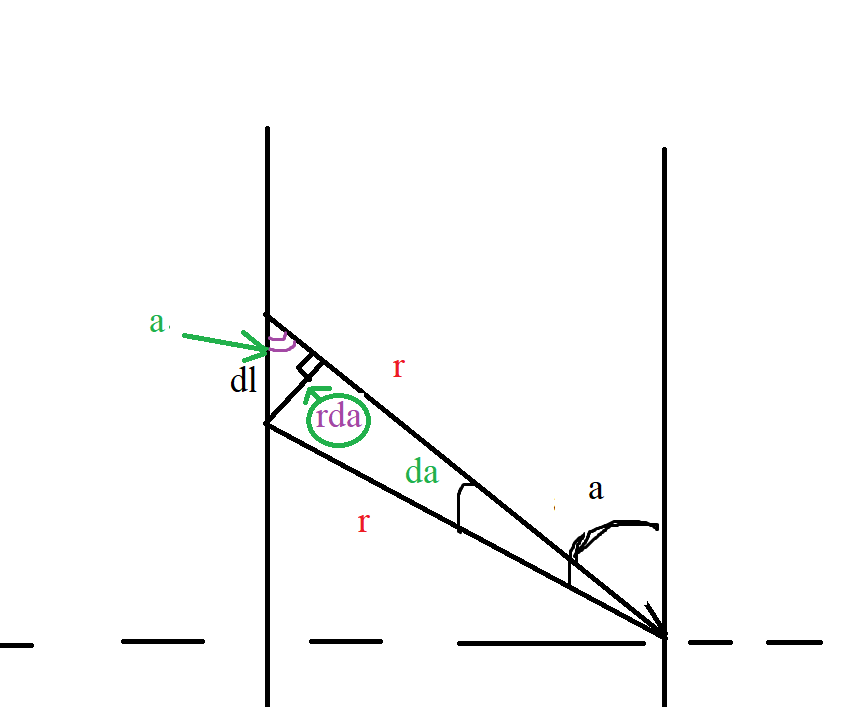
и простой для него случай нарисуем вот так:
Из рисунка по геометрии видно, что:
r=\frac{L_0}{\sin{\alpha}}\\
dl=\frac{r\alpha}{\sin{\alpha}}=\frac{L_0d\alpha}{\sin^2{\alpha}}
Подставляем в ранее выше формулу и получается:
B=\frac{\mu\mu_0}{4\pi}I\int\frac{L_0d\alpha\space{\sin^2\alpha}}{\sin^2{\alpha{L_0^2}}}=\frac{\mu\mu_0}{4\pi}\frac{I}{L_0}\int\limits_{\alpha_1}^{\alpha_2}{\sin{\alpha}d\alpha}
Получается красивая формула из закона Био-Савара-Лапласса:
B=\frac{\mu\mu_0I}{4\pi{L_0}}(\cos{\alpha_1}-\cos{\alpha_2})
Почему у тебя первый угол равен 135°?
Обрати внимание на что такой такой угол никак не соответствует такому значению.
Попробуй изобразить все таким образом и подумать, как можно описать угол для точек:
3 лайка
Такой не может использоваться для первой точки и тут сам угол будет равен 45°.
Я про 2 точку
1 лайк
Если хочешь рассматривать относительно второй точки, то у тебя второй угол не будет равен 0. Мой рисунок чуть чуть не правильный, его нужно смотреть под таким углом.
1 лайк
А где расположен 2 угол?Разве провод не заканчивается на месте сгиба.
Внимательно посмотри на свой поставленный угол и попробуй подумать почему мы не можем сделать второй угол внутри бесконечного треугольника.
@28128 разобрался?
1 лайк
Нет, не понял
Я не понял уравнения dl=ra/sina
Сможете это объяснить?
В этой формуле у вас В=(uu0I/4π)S[L0dasin²a/sin²aL0²]
От сюда почему в интеграле вышло sinada
sin²a сокротятся же?
S–интеграл
Во первых, да ,ошибочка, не просто угол \alpha, а бесконечно малый угол d\alpha
Во вторых, Посмотрите еще раз на рисунок, если распишите все от точки до атомов, то полный рисунок выглядит вот так:
Тут судя по рисунку я указал, где и будет у нас длина rd\alpha, если шире посмотреть на линии и углы, то не сложно можно определить, что в треугольнике rd\alpha и dl можно расположить наш основной угол \alpha. Если погрузимся, то в масштабы еще меньше рисунка, то увеличиваем наш созданный треугольник так:
По геометрии определяем соотношение:
\sin{\alpha}=\frac{rd\alpha}{dl}\\
dl=\frac{rda}{\sin{\alpha}}
Тут важно знать, суть как надо понять слово “бесконечно малый” угол и
Если до конца расписать формулу:
B=\frac{\mu\mu_0}{4\pi}I\int\frac{\sin{\alpha}}{r^2}dl\\
Используем найденные данные с рисунка в данную формулу и находим формулу магнитной индукции:
B=\frac{\mu\mu}{4\pi}I\int\frac{\sin{\alpha\cdot\sin^2{\alpha}}}{L_0^2}\cdot\frac{L_0d\alpha}{\sin^2{\alpha}}\\
\space\\
B=\frac{\mu\mu}{4\pi{L_0}}I\int\sin{\alpha{d\alpha}}
Дальше уже берете лимиты от \alpha_1 до \alpha_2 и выводите ту же формулу.
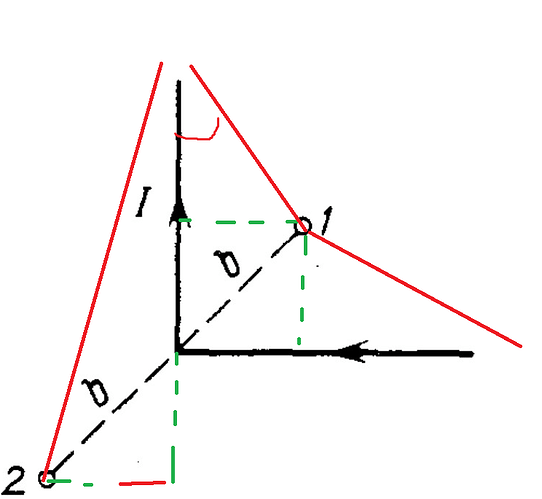
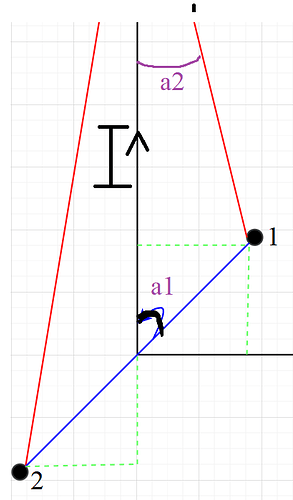
Дальше я бы хотел убедиться, что все решение понятно и до этого понятно. Берем два случая для рассмотрения первое относительно первой точки, второе относительно другой точки.
Для первого случая рисунок выглядит вот так:
Очевидно, что если мы берем первую точку, то первый угол под 45\degree, а второй угол уходит в бесконечность далекий и малый угол примерно 0. Принцип суперпозиции магнитных полей(советую по больше изучить этот принцип) объясняет эти углы.
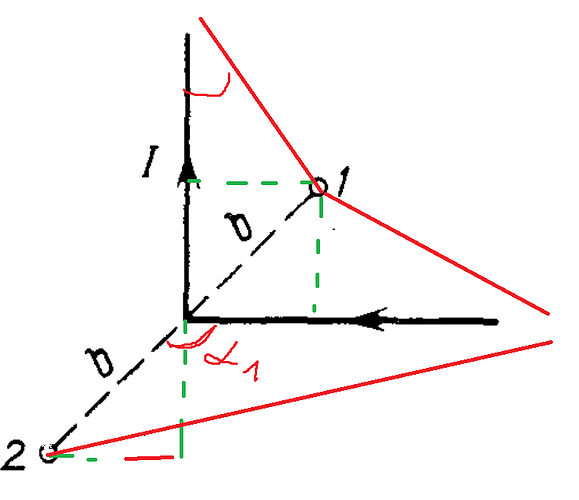
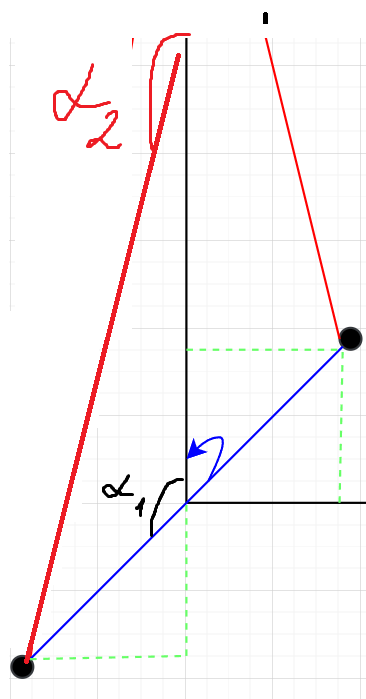
Для второго угла используется тот же принцип суперпозиции магнитных полей, то чуть другим образом:
Если посмотреть на рисунок, то первый угол будет равен 135\degree, а второй угол также уходит в бесконечность, но при этом бесконечно раз растет до угла \pi, тем самым видно, что обе угла выступают снаружи “треугольников”.
Какую бы мы не брали точку, используя формулу Био-Савара-Лапласса выходит один и тот же ответ, только в противоложных значениях.
7 лайков
Спасибо
2 лайка